Magsiyasat ng isang function para sa pagpapatuloy at bumuo ng isang graph online. Paano mag-imbestiga ng isang function para sa pagpapatuloy

Halimbawa 1 Patunayan na ang function na y=sinx ay tuloy-tuloy para sa anumang halaga ng x.
Solusyon. Hayaang ang x 0 ay isang arbitrary na punto. Ang pagbibigay nito ng dagdag na Δx, nakukuha natin ang puntong x=x 0 +Δx. Pagkatapos . Nakukuha namin .
Kahulugan. Ang function na y=f(x) ay tinatawag na tuloy-tuloy sa puntong x 0 sa kanan (kaliwa) kung
.
Ang isang function na tuloy-tuloy sa isang panloob na punto ay parehong kanan at kaliwa tuloy-tuloy. Totoo rin ang kabaligtaran: kung ang isang function ay tuloy-tuloy sa isang punto sa kaliwa at kanan, ito ay magiging tuluy-tuloy sa puntong iyon. Gayunpaman, ang function ay maaari lamang maging tuloy-tuloy sa isang panig. Halimbawa, para sa , , f(1)=1, samakatuwid, ang function na ito ay tuloy-tuloy lamang sa kaliwa (para sa graph ng function na ito, tingnan ang Seksyon 5.7.2 sa itaas).
Kahulugan. Ang isang function ay tinatawag na tuloy-tuloy sa ilang pagitan kung ito ay tuloy-tuloy sa bawat punto ng pagitan na ito.
Sa partikular, kung ang pagitan ay isang segment , kung gayon ang isang panig na pagpapatuloy ay ipinahiwatig sa mga dulo nito.

Mga katangian ng tuluy-tuloy na pag-andar

Mga function break at ang kanilang pag-uuri

Ang sumusunod na klasipikasyon ay tinatanggap para sa mga discontinuity point.
1) Kung sa puntong x 0 ay may hangganan At , ngunit f(x 0 +0)≠f(x 0 -0), pagkatapos x 0 ay tinatawag breaking point ng unang uri , habang tumatawag sila function na tumalon .

Halimbawa 2 Isaalang-alang ang function
Ang break ng function ay posible lamang sa puntong x=2 (sa ibang mga punto ito ay tuluy-tuloy tulad ng anumang polynomial).
Hanapin natin , . Dahil ang mga one-sided na limitasyon ay may hangganan, ngunit hindi katumbas ng bawat isa, sa puntong x=2 ang function ay may discontinuity ng unang uri. pansinin mo yan , kaya ang function ay right-continuous sa puntong ito (Fig. 2).
2) Mga discontinuity point ng pangalawang uri Tinatawag ang mga puntos kung saan ang hindi bababa sa isa sa mga one-sided na limitasyon ay katumbas ng ∞ o wala.

Halimbawa 3 Ang function na y=2 1/ x ay tuloy-tuloy para sa lahat ng value ng x, maliban sa x=0. Maghanap ng mga one-sided na limitasyon: , , kaya ang x=0 ay isang discontinuity point ng pangalawang uri (Fig. 3).
3) Ang puntong x=x 0 ay tinatawag break point , kung f(x 0 +0)=f(x 0 -0)≠f(x 0).
Ang puwang ay "naaalis" sa kahulugan na sapat na upang baguhin (muling tukuyin o muling tukuyin) ang halaga ng function sa puntong ito sa pamamagitan ng pagtatakda , at ang function ay magiging tuluy-tuloy sa puntong x 0 .
Halimbawa 4 Ito ay kilala na , at ang limitasyong ito ay hindi nakadepende sa kung paano nagiging zero ang x. Ngunit ang pag-andar sa puntong x=0 ay hindi tinukoy. Kung palawigin natin ang kahulugan ng function sa pamamagitan ng pagtatakda ng f(0)=1, kung gayon ito ay magiging tuloy-tuloy sa puntong ito (sa ibang mga punto ito ay tuloy-tuloy bilang isang quotient ng tuloy-tuloy na mga function ng sinx at x).
Halimbawa 5 Magsiyasat para sa pagpapatuloy ng isang function .
Solusyon. Ang mga function na y=x 3 at y=2x ay tinukoy at tuluy-tuloy sa lahat ng dako, kasama ang mga ipinahiwatig na pagitan. Suriin natin ang junction point ng mga gaps x=0:
, , . Nakukuha namin iyon , kung saan sumusunod na sa puntong x=0 ang function ay tuloy-tuloy.
Kahulugan. Ang isang function na tuluy-tuloy sa isang interval maliban sa isang may hangganang bilang ng mga discontinuity ng unang uri o isang naaalis na discontinuity ay sinasabing piecewise continuous sa interval na ito.

Mga halimbawa ng hindi tuloy-tuloy na function

Halimbawa 4 Posible bang alisin ang mga break sa mga function:
ngunit) sa puntong x=2;
b) sa puntong x=2;
sa) sa puntong x=1?
Solusyon. Tungkol sa halimbawa a), maaari nating agad na sabihin na ang discontinuity f(x) sa puntong x=2 ay hindi maaaring alisin, dahil may mga walang katapusang one-sided na limitasyon sa puntong ito (tingnan ang halimbawa 1).
b) Ang function na g(x) bagama't may finite one-sided na limitasyon sa puntong x=2

(,),

Halimbawa 5 Ipakita na ang Dirichlet function

Halimbawa 6 Maghanap ng mga function break point

Para sa malayang desisyon.
Siyasatin ang mga function para sa continuity at tukuyin ang uri ng mga discontinuity point:
1) ; Sagot: x=-1 – break point;
2) ; Sagot: Discontinuity ng pangalawang uri sa puntong x=8;
3) ; Sagot: Discontinuity ng unang uri sa x=1;
4)
Sagot: Sa punto x 1 \u003d -5 mayroong isang naaalis na puwang, sa x 2 \u003d 1 - isang puwang ng pangalawang uri at sa punto x 3 \u003d 0 - isang puwang ng unang uri.
5) Paano dapat piliin ang numero A upang ang function

magiging tuluy-tuloy sa puntong x=0?
Sagot: A=2.
6) Posible bang piliin ang numero A upang ang function

magiging tuluy-tuloy sa puntong x=2?
Sagot: hindi.

Continuity at Graphing ng Piecewise Defined Function − mahirap na paksa. Mas mainam na matutunan kung paano bumuo ng mga graph nang direkta sa isang praktikal na aralin. Dito, pangunahing ipinapakita ang pag-aaral sa pagpapatuloy.

Ito ay kilala na elementarya function(tingnan ang p. 16) ay tuloy-tuloy sa lahat ng punto kung saan ito ay tinukoy. Samakatuwid, ang discontinuity sa elementarya na pag-andar posible lamang sa dalawang uri ng mga punto:

a) sa mga punto kung saan ang function ay "na-override";

b) sa mga punto kung saan wala ang function.

Alinsunod dito, ang mga naturang punto lamang ang sinusuri para sa pagpapatuloy sa panahon ng pag-aaral, tulad ng ipinapakita sa mga halimbawa.

Para sa mga non-elementary functions, ang pag-aaral ay mas mahirap. Halimbawa, ang isang function (ang integer na bahagi ng isang numero) ay tinukoy sa buong linya ng numero, ngunit dumaranas ng break sa bawat integer x. Ang mga tanong na tulad nito ay nasa labas ng saklaw ng gabay na ito.

Bago pag-aralan ang materyal, dapat mong ulitin mula sa isang panayam o aklat-aralin kung ano (anong uri) ang mga break point.

Pagsisiyasat ng pira-pirasong ibinigay na mga function para sa pagpapatuloy

Set ng function pira-piraso, kung ito ay ibinibigay ng iba't ibang mga formula sa iba't ibang bahagi ng domain ng kahulugan.

Ang pangunahing ideya sa pag-aaral ng mga naturang function ay upang malaman kung ang function ay tinukoy sa mga punto kung saan ito ay muling tinukoy, at kung paano. Pagkatapos ay sinusuri kung ang mga halaga ng pag-andar sa kaliwa at sa kanan ng naturang mga punto ay pareho.

Halimbawa 1 Ipakita natin na ang function
tuloy-tuloy.

Function
ay elementarya at samakatuwid ay tuloy-tuloy sa mga punto kung saan ito tinukoy. Ngunit, malinaw naman, ito ay tinukoy sa lahat ng mga punto. Samakatuwid, ito ay tuloy-tuloy sa lahat ng mga punto, kabilang ang sa
, ayon sa kinakailangan ng kondisyon.

Ang parehong ay totoo para sa pag-andar
, at sa
ito ay tuloy-tuloy.

Sa ganitong mga kaso, ang pagpapatuloy ay maaari lamang masira kung saan ang function ay muling tinukoy. Sa aming halimbawa, ito ang punto
. Suriin natin ito, kung saan makikita natin ang mga limitasyon sa kaliwa at kanan:

Ang mga limitasyon sa kaliwa at kanan ay pareho. Ito ay nananatiling makikita:

a) kung ang function ay tinukoy sa mismong punto
;

b) kung gayon, tumutugma ba ito?
na may mga halaga ng limitasyon sa kaliwa at kanan.

Sa kondisyon, kung
, pagkatapos
. kaya lang
.

Nakikita natin iyan (lahat ay katumbas ng numero 2). Nangangahulugan ito na sa puntong iyon
tuloy-tuloy ang function. Kaya ang pag-andar ay tuloy-tuloy sa buong axis, kabilang ang punto
.

Mga Tala ng Solusyon

a) Hindi ito gumanap ng papel sa mga kalkulasyon, kapalit tayo ay nasa isang tiyak na formula ng numero
o
. Ito ay karaniwang mahalaga kapag ang paghahati sa isang infinitesimal na halaga ay nakuha, dahil ito ay nakakaapekto sa tanda ng infinity. Dito
At
responsable lamang para sa pagpili ng function;

b) bilang panuntunan, mga pagtatalaga
At
ay pantay, ang parehong naaangkop sa mga pagtatalaga
At
(at totoo para sa anumang punto, hindi lamang para sa
). Sa mga sumusunod, para sa kaiklian, ginagamit namin ang mga notasyon ng form
;

c) kapag ang mga limitasyon sa kaliwa at sa kanan ay pantay, upang subukan para sa pagpapatuloy, sa katunayan, ito ay nananatiling upang makita kung ang isa sa mga hindi pagkakapantay-pantay maluwag. Sa halimbawa, ito ay naging ika-2 hindi pagkakapantay-pantay.

Halimbawa 2 Sinisiyasat namin ang pagpapatuloy ng function
.

Para sa parehong mga kadahilanan tulad ng sa Halimbawa 1, ang pagpapatuloy ay maaari lamang masira sa punto
. Suriin natin:

Ang mga limitasyon sa kaliwa at kanan ay pantay, ngunit sa punto mismo
ang pag-andar ay hindi tinukoy (ang mga hindi pagkakapantay-pantay ay mahigpit). Ibig sabihin nito ay
- tuldok naaayos na puwang.

Ang ibig sabihin ng "Removable discontinuity" ay sapat na upang gawing hindi mahigpit ang alinman sa mga hindi pagkakapantay-pantay, o mag-imbento para sa isang hiwalay na punto
function, ang halaga nito sa
ay -5, o ipahiwatig lang iyon
upang ang buong pag-andar
naging tuloy-tuloy.

Sagot: tuldok
– break point.

Puna 1. Sa panitikan, ang isang naaalis na puwang ay karaniwang itinuturing na isang espesyal na kaso ng isang puwang ng unang uri, gayunpaman, ang mga mag-aaral ay mas madalas na nauunawaan bilang isang hiwalay na uri ng puwang. Upang maiwasan ang mga pagkakaiba, susundin namin ang 1st point of view, at partikular naming itatakda ang "irremovable" gap ng 1st kind.

Halimbawa 3 Suriin kung tuloy-tuloy ang function

Sa punto

Magkaiba ang mga limitasyon sa kaliwa at kanan:
. Natukoy man o hindi ang function
(oo) at kung gayon, kung ano ang katumbas ng (ay katumbas ng 2), punto
–punto ng hindi naaalis na discontinuity ng 1st kind.

Sa punto
nangyayari huling pagtalon(mula 1 hanggang 2).

Sagot: tuldok

Puna 2. sa halip na
At
karaniwang nagsusulat
At
ayon sa pagkakabanggit.

Available tanong: paano naiiba ang mga pag-andar

At
,

at pati na rin ang kanilang mga tsart? Tama sagot:

a) Ang 2nd function ay hindi tinukoy sa punto
;

b) sa graph ng 1st function, ang punto
"painted over", sa graph 2 - hindi ("punctured point").

Dot
kung saan nagtatapos ang graph
, ay hindi naka-shade sa parehong mga graph.

Mas mahirap pag-aralan ang mga function na naiiba ang kahulugan sa tatlo mga plot.

Halimbawa 4 Tuloy-tuloy ba ang pag-andar?
?

Tulad ng sa mga halimbawa 1 - 3, bawat isa sa mga function
,
At ay tuloy-tuloy sa buong numerical axis, kasama ang seksyon kung saan ito ibinigay. Ang puwang ay posible lamang sa punto
o (at) sa punto
kung saan na-override ang function.

Ang gawain ay nahahati sa 2 subtasks: upang siyasatin ang pagpapatuloy ng function

At
,

saka, ang punto
hindi interesado sa function
, at ang punto
- para sa function
.

1st step. Sinusuri ang punto
at function
(hindi namin isinusulat ang index):

Ang mga limitasyon ay tumutugma. Sa kondisyon,
(kung ang mga limitasyon sa kaliwa at sa kanan ay pantay, kung gayon ang pag-andar ay aktwal na tuluy-tuloy kapag ang isa sa mga hindi pagkakapantay-pantay ay hindi mahigpit). Kaya sa punto
tuloy-tuloy ang function.

ika-2 hakbang. Sinusuri ang punto
at function
:

Sa abot ng
, tuldok
ay isang discontinuity point ng unang uri, at ang halaga
(at kung mayroon man) ay hindi na mahalaga.

Sagot: ang function ay tuloy-tuloy sa lahat ng mga punto maliban sa punto
, kung saan mayroong hindi mababawi na pagkaputol ng unang uri - isang pagtalon mula 6 hanggang 4.

Halimbawa 5 Maghanap ng mga function break point
.

Kumilos kami sa parehong paraan tulad ng sa halimbawa 4.

1st step. Sinusuri ang punto
:

ngunit)
, dahil sa kaliwa ng
ang function ay pare-pareho at katumbas ng 0;

b) (
ay isang pantay na pag-andar).

Ang mga limitasyon ay pareho, ngunit
ang pag-andar ay hindi tinukoy ng kundisyon, at ito ay lumalabas na
– break point.

ika-2 hakbang. Sinusuri ang punto
:

ngunit)
;

b)
- ang halaga ng function ay hindi nakadepende sa variable.

Ang mga limitasyon ay iba: , tuldok
ay ang punto ng hindi matatanggal na discontinuity ng unang uri.

Sagot:
- break point,
ay isang punto ng hindi naaalis na discontinuity ng unang uri, sa iba pang mga punto ang function ay tuloy-tuloy.

Halimbawa 6 Tuloy-tuloy ba ang pag-andar?
?

Function
tinutukoy sa
, kaya ang kondisyon
nagiging kondisyon
.

Sa kabilang banda, ang pag-andar
tinutukoy sa
, ibig sabihin. sa
. Kaya ang kondisyon
nagiging kondisyon
.

Ito ay lumiliko na ang kondisyon ay dapat masiyahan
, at ang domain ng kahulugan ng buong function ay ang segment
.

Ang mga function mismo
At
ay elementarya at samakatuwid ay tuluy-tuloy sa lahat ng mga punto kung saan ang mga ito ay tinukoy—sa partikular, at para sa
.

Ito ay nananatiling suriin kung ano ang nangyayari sa punto
:

ngunit)
;

Sa abot ng
, tingnan kung ang function ay tinukoy sa punto
. Oo, ang 1st inequality ay hindi mahigpit na may kinalaman sa
, at sapat na iyon.

Sagot: ang function ay tinukoy sa pagitan
at tuloy-tuloy dito.

Ang mas kumplikadong mga kaso, kapag ang isa sa mga constituent function ay hindi elementarya o hindi tinukoy sa anumang punto sa segment nito, ay lampas sa saklaw ng manual.

NF1. I-plot ang mga function graph. Bigyang-pansin kung ang function ay tinukoy sa punto kung saan ito ay muling tinukoy, at kung gayon, ano ang halaga ng function (ang salitang " kung” ay tinanggal sa kahulugan ng function para sa kaiklian):

1) a)
b)
sa)
G)

2) a)
b)
sa)
G)

3) a)
b)
sa)
G)

4) a)
b)
sa)
G)

Halimbawa 7 Hayaan
. Pagkatapos sa site
bumuo ng isang pahalang na linya
, at sa balangkas
bumuo ng isang pahalang na linya
. Sa kasong ito, ang punto na may mga coordinate
"gouged out" at ang tuldok
"pininturahan". Sa punto
ang isang discontinuity ng 1st kind ("jump") ay nakuha, at
.

NF2. Siyasatin para sa pagpapatuloy ang mga function na tinukoy nang naiiba sa 3 agwat. I-plot ang mga graph:

1) a)
b)
sa)

G)
e)
e)

2) a)
b)
sa)

G)
e)
e)

3) a)
b)
sa)

G)
e)
e)

Halimbawa 8 Hayaan
. Lokasyon sa
bumuo ng isang tuwid na linya
, kung saan matatagpuan namin
At
. Pagkonekta ng mga tuldok
At
segment. Hindi namin isinama ang mga puntos sa kanilang sarili, dahil para sa
At
ang function ay hindi tinukoy ng kundisyon.

Naka-on ang lokasyon
At
bilugan ang OX axis (nasa ito
), ngunit ang mga puntos
At
"natumba". Sa punto
nakakakuha kami ng isang naaalis na discontinuity, at sa punto
– discontinuity ng 1st kind (“tumalon”).

NF3. I-plot ang mga function graph at tiyaking tuluy-tuloy ang mga ito:

1) a)
b)
sa)

G)
e)
e)

2) a)
b)
sa)

G)
e)
e)

NF4. Tiyaking tuloy-tuloy ang mga function at buuin ang kanilang mga graph:

1) a)
b)
sa)

2 a)
b)
sa)

3) a)
b)
sa)

NF5. I-plot ang mga function graph. Bigyang-pansin ang pagpapatuloy:

1) a)
b)
sa)

G)
e)
e)

2) a)
b)
sa)

G)
e)
e)

3) a)
b)
sa)

G)
e)
e)

4) a)
b)
sa)

G)
e)
e)

5) a)
b)
sa)

G)
e)
e)

NF6. I-plot ang mga graph ng mga hindi tuluy-tuloy na function. Tandaan ang halaga ng function sa punto kung saan muling tinukoy ang function (at kung mayroon man ito):

1) a)
b)
sa)

G)
e)
e)

2) a)
b)
sa)

G)
e)
e)

3) a)
b)
sa)

G)
e)
e)

4) a)
b)
sa)

G)
e)
e)

5) a)
b)
sa)

G)
e)
e)

NF7. Parehong gawain tulad ng sa NF6:

1) a)
b)
sa)

G)
e)
e)

2) a)
b)
sa)

G)
e)
e)

3) a)
b)
sa)

G)
e)
e)

4) a)
b)
sa)

G)
e)
e)

Pagtukoy sa break point ng isang function
dulong punto x 0 tinawag function break point f (x), kung ang function ay tinukoy sa ilang nabutas na kapitbahayan ng puntong x 0 , ngunit hindi tuloy-tuloy sa puntong iyon.

Ibig sabihin, sa punto ng discontinuity, ang function ay maaaring hindi tinukoy o tinukoy, ngunit hindi bababa sa isang one-sided na limitasyon sa puntong ito ay alinman ay hindi umiiral, o hindi katumbas ng halaga f (x0) function sa point x 0 . Tingnan ang "Pagtukoy sa pagpapatuloy ng isang function sa isang punto".

Pagpapasiya ng break point ng 1st kind
Tinatawag ang punto breaking point ng unang uri, kung ay isang breakpoint at may may hangganang one-sided na limitasyon sa kaliwa at sa kanan:
.

Depinisyon ng pagtalon ng function
Tumalon Δ function sa isang punto ay tinatawag na pagkakaiba sa pagitan ng mga limitasyon sa kanan at sa kaliwa
.

Pagtukoy ng break point
Tinatawag ang punto break point kung may limitasyon
,
ngunit ang function sa punto ay alinman sa hindi tinukoy o hindi katumbas ng limitasyong halaga: .

Kaya, ang isang maaaring iurong na discontinuity point ay isang discontinuity point ng unang uri, kung saan ang jump ng function ay katumbas ng zero.

Pagpapasiya ng break point ng ika-2 uri
Ang breaking point ay tinatawag breaking point ng pangalawang uri, kung hindi ito isang discontinuity point ng 1st kind. Ibig sabihin, kung walang kahit isang one-sided na limitasyon, o kahit isang one-sided na limitasyon sa isang punto ay katumbas ng infinity.

Pagsisiyasat ng mga function para sa pagpapatuloy

Kapag nag-iimbestiga ng mga function para sa pagpapatuloy, ginagamit namin ang mga sumusunod na katotohanan.

• Mga Tungkulin sa Elementarya at ang kanilang mga kabaligtaran ay tuloy-tuloy sa kanilang domain ng kahulugan. Kabilang dito ang mga sumusunod na tampok:
  , pati na rin ang pare-pareho at ang kanilang mga kabaligtaran na pag-andar. Tingnan ang "Sanggunian sa Mga Elementarya na Function".
• Kabuuan, pagkakaiba at produkto Ang tuluy-tuloy, sa ilang hanay ng mga function, ay isang tuluy-tuloy, function sa set na ito.
  Pribado ng dalawang tuloy-tuloy, sa ilang hanay ng mga function, ay isang tuluy-tuloy, function sa set na ito, maliban sa mga punto kung saan nawawala ang denominator ng fraction. Tingnan ang "Arithmetic Properties of Continuous Functions"
• Kumplikadong function ay tuloy-tuloy sa isang punto kung ang function ay tuloy-tuloy sa isang punto at ang function ay tuloy-tuloy sa isang punto. Tingnan ang "Limit at pagpapatuloy ng isang compound function"

Mga halimbawa

Halimbawa 1

Ibinigay ang isang function at dalawang halaga ng argumento at . Kinakailangan: 1) upang matukoy kung ibinigay na function tuloy-tuloy o hindi tuloy-tuloy para sa bawat ibinigay na halaga ng argumento; 2) sa kaso ng isang function break, hanapin ang mga limitasyon nito sa break point sa kaliwa at kanan, itakda ang uri ng break; 3) gumawa ng isang eskematiko na pagguhit.
.

Ang ibinigay na function ay kumplikado. Maaari itong tingnan bilang isang komposisyon ng dalawang function:
, . Pagkatapos
.

Isaalang-alang natin ang isang function. Binubuo ito ng isang function at constants gamit ang arithmetic operations ng karagdagan at paghahati. Ang function ay isang elementary - power function na may exponent 1 . Ito ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable. Samakatuwid, ang function ay tinukoy at tuloy-tuloy para sa lahat , maliban sa mga punto kung saan ang denominator ng fraction ay naglalaho. Itinutumbas namin ang denominator sa zero at lutasin ang equation:
.
Kumuha kami ng isang ugat.
Kaya, ang function ay tinukoy at tuloy-tuloy para sa lahat maliban sa punto .

Isaalang-alang natin ang isang function. Isa itong exponential function na may positibong base. Ito ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable.
kaya lang ibinigay na function ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable, maliban sa punto.

Kaya, sa punto , ang ibinigay na function ay tuloy-tuloy.

Graph ng function na y = 4 1/(x+2).

Isaalang-alang natin ang isang punto. Sa puntong ito, ang function ay hindi tinukoy. Samakatuwid, hindi ito tuluy-tuloy. Itatag natin ang uri ng discontinuity. Para magawa ito, nakakahanap kami ng mga one-sided na limitasyon.

Gamit ang koneksyon sa pagitan ng walang katapusan na malaki at walang katapusan na maliliit na function, para sa limitasyon sa kaliwa mayroon kaming:
sa ,
,
,
.

Dito ginamit namin ang sumusunod na karaniwang notasyon:
.
Ginamit din namin ang ari-arian exponential function may base:
.

Katulad nito, para sa limitasyon sa kanan mayroon kaming:
sa ,
,
,
.

Dahil ang isa sa mga one-sided na limitasyon ay katumbas ng infinity, mayroong isang discontinuity ng pangalawang uri sa punto.

Sa isang punto, ang function ay tuloy-tuloy.
Sa punto ng hindi pagpapatuloy ng pangalawang uri,
.

Halimbawa 2

Nakatakda ang function. Maghanap ng mga breakpoint ng function, kung mayroon sila. Ipahiwatig ang uri ng break at jumps ng function, kung mayroon man. Gumawa ng drawing.
.

Graph ng isang ibinigay na function.

Ang function ay function ng kapangyarihan na may integer exponent na katumbas ng 1 . Ang ganitong function ay tinatawag ding linear function. Ito ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable.

May dalawa pang function na kasama: at . Binubuo ang mga ito ng isang function at constants gamit ang arithmetic operations ng karagdagan at multiplikasyon:
, .
Samakatuwid sila ay tuloy-tuloy din para sa lahat.

Dahil ang mga function na kasama sa komposisyon ay tuluy-tuloy para sa lahat, maaari itong magkaroon ng mga discontinuity point lamang sa mga gluing point ng mga bahagi nito. Ito ay mga puntos at . Sinisiyasat namin para sa pagpapatuloy sa mga puntong ito. Para magawa ito, nakakahanap kami ng mga one-sided na limitasyon.

Isaalang-alang natin ang isang punto. Upang mahanap ang kaliwang limitasyon ng isang function sa puntong ito, dapat nating gamitin ang mga halaga ng function na ito sa anumang kaliwang butas na kapitbahayan ng punto. Kunin natin ang kapitbahayan. sa kanya. Pagkatapos ang limitasyon sa kaliwa:
.
Dito ginamit namin ang katotohanan na ang function ay tuloy-tuloy sa isang punto (tulad ng sa anumang iba pang punto). Samakatuwid, ang kaliwa (at kanan) na limitasyon nito ay katumbas ng halaga ng function sa puntong ito.

Hanapin ang tamang limitasyon sa punto. Upang gawin ito, dapat nating gamitin ang mga halaga ng function sa anumang tamang butas na kapitbahayan ng puntong ito. Kunin natin ang kapitbahayan. sa kanya. Pagkatapos ang limitasyon sa kanan:
.
Dito rin namin ginamit ang pagpapatuloy ng function .

Dahil, sa puntong , ang limitasyon sa kaliwa ay hindi katumbas ng limitasyon sa kanan, kung gayon ang function sa loob nito ay hindi tuloy-tuloy - ito ang break point. Dahil may hangganan ang isang panig na limitasyon, ito ay isang discontinuity point ng unang uri. Tumalon function:
.

Ngayon isaalang-alang ang isang punto. Sa parehong paraan, kinakalkula namin ang isang panig na limitasyon:
;
.
Dahil ang function ay tinukoy sa isang punto at ang kaliwang limitasyon ay katumbas ng kanan, ang function ay tuloy-tuloy sa puntong ito.

Ang function ay may discontinuity ng unang uri sa punto . Tumalon ang function dito: . Sa iba pang mga punto, ang pag-andar ay tuloy-tuloy.

Halimbawa 3

Tukuyin ang mga discontinuity point ng function at siyasatin ang katangian ng mga puntong ito kung
.

Gamitin natin ang katotohanan na ang linear function ay tinukoy at tuloy-tuloy para sa lahat. Ang tinukoy na function ay binubuo ng isang linear function at constants gamit ang arithmetic operations ng karagdagan, pagbabawas, multiplikasyon, at paghahati:
.
Samakatuwid, ito ay tinukoy at tuloy-tuloy para sa lahat , maliban sa mga punto kung saan nawawala ang denominator ng fraction.

Hanapin natin ang mga puntong ito. Itinutumbas namin ang denominator sa zero at lutasin ang quadratic equation:
;
;
; .
Pagkatapos
.

Ginagamit namin ang formula:
.
Sa tulong nito, nabubulok namin ang numerator sa mga salik:
.

Pagkatapos ang ibinigay na function ay kukuha ng form:
(P1) .
Ito ay tinukoy at tuloy-tuloy para sa lahat maliban sa mga punto at . Samakatuwid, ang mga punto at ang mga discontinuity point ng function.

Hatiin ang numerator at denominator ng fraction sa (P1) sa pamamagitan ng:
(P2) .
Magagawa natin ang operasyong ito kung . Sa ganitong paraan,
sa .
Iyon ay, ang mga function at naiiba lamang sa isang punto: ito ay tinukoy sa , ngunit hindi ito tinukoy sa puntong ito.

Upang matukoy ang genus ng mga breakpoint, kailangan nating hanapin ang mga one-sided na limitasyon ng function sa mga punto at . Upang kalkulahin ang mga ito, gagamitin namin ang katotohanan na kung ang mga halaga ng function ay binago, o ginawang hindi natukoy sa isang may hangganan na bilang ng mga puntos, kung gayon hindi ito magkakaroon ng anumang epekto sa halaga o pagkakaroon ng limitasyon sa isang arbitrary na punto. (tingnan ang "Impluwensiya ng mga halaga ng function sa isang may hangganang bilang ng mga puntos sa halaga ng limitasyon "). Iyon ay, ang mga limitasyon ng function sa anumang mga punto ay katumbas ng mga limitasyon ng function.

Isaalang-alang natin ang isang punto. Ang denominator ng fraction sa function na , at ay hindi naglalaho. Samakatuwid, ito ay tinukoy at tuloy-tuloy para sa . Ito ay nagpapahiwatig na mayroong limitasyon sa at ito ay katumbas ng halaga ng function sa puntong ito:
.
Samakatuwid, ang punto ay isang discontinuity point ng unang uri.

Isaalang-alang natin ang isang punto. Gamit ang koneksyon ng infinitesimal at infinitely large functions , mayroon kaming:
;
.
Dahil ang mga limitasyon ay walang hanggan, mayroong isang discontinuity ng pangalawang uri sa puntong ito.

Ang function ay may discontinuity point ng unang uri sa , at isang discontinuity point ng pangalawang uri sa .

Mga sanggunian:
O.I. Mga demonyo. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004.

Sa araling ito, matututunan natin kung paano itatag ang pagpapatuloy ng isang function. Gagawin namin ito sa tulong ng mga limitasyon, bukod pa rito, isang panig - kanan at kaliwa, na hindi naman nakakatakot, sa kabila ng katotohanan na ang mga ito ay nakasulat bilang at .

Ngunit ano ang pagpapatuloy ng isang function sa pangkalahatan? Hanggang sa makarating tayo sa isang mahigpit na kahulugan, ang pinakamadaling paraan upang isipin ang isang linya na maaaring iguhit nang hindi inaangat ang lapis mula sa papel. Kung ang gayong linya ay iguguhit, pagkatapos ito ay tuloy-tuloy. Ang linyang ito ay ang graph ng isang tuluy-tuloy na function.

Sa graphically, ang isang function ay tuloy-tuloy sa isang punto kung ang graph nito ay hindi "masira" sa puntong iyon. Ang graph ng naturang tuluy-tuloy na function ay ipinapakita sa figure sa ibaba.

Kahulugan ng pagpapatuloy ng isang function sa pamamagitan ng limitasyon. Ang isang function ay tuloy-tuloy sa isang punto sa ilalim ng tatlong kundisyon:

1. Ang function ay tinukoy sa puntong .

Kung hindi matugunan ang kahit isa sa mga kundisyon sa itaas, ang function ay hindi tuloy-tuloy sa isang punto. Kasabay nito, sinasabi nila na ang function ay dumaranas ng break, at ang mga punto sa graph kung saan ang graph ay nagambala ay tinatawag na break point ng function. Ang graph ng naturang function, na dumaranas ng break sa puntong x=2, ay ipinapakita sa figure sa ibaba.

Halimbawa 1 Function f(x) ay tinukoy bilang mga sumusunod:

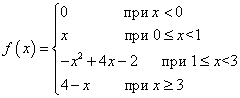
Magiging tuloy-tuloy ba ang pagpapaandar na ito sa bawat hangganan ng mga sanga nito, iyon ay, sa mga punto x = 0 , x = 1 , x = 3 ?

Solusyon. Sinusuri namin ang lahat ng tatlong kundisyon para sa pagpapatuloy ng pag-andar sa bawat boundary point. Ang unang kundisyon ay natutugunan dahil tinukoy ang function sa bawat isa sa mga boundary point ay sumusunod mula sa kahulugan ng function. Ito ay nananatiling suriin ang natitirang dalawang kondisyon.

Dot x= 0 . Hanapin ang kaliwang limitasyon sa puntong ito:

.

Hanapin natin ang limitasyon sa kanang kamay:

x= 0 ay dapat matagpuan sa sangay ng function na kinabibilangan ng puntong ito, iyon ay, ang pangalawang sangay. Natagpuan namin sila:

Tulad ng makikita mo, ang limitasyon ng function at ang halaga ng function sa punto x= 0 ay katumbas. Samakatuwid, ang pag-andar ay tuloy-tuloy sa punto x = 0 .

Dot x= 1 . Hanapin ang kaliwang limitasyon sa puntong ito:

Hanapin natin ang limitasyon sa kanang kamay:

Limitasyon sa pag-andar at halaga ng pag-andar sa isang punto x= 1 ay dapat matagpuan sa sangay ng function na kinabibilangan ng puntong ito, iyon ay, ang pangalawang sangay. Natagpuan namin sila:

.

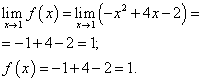Limitasyon sa pag-andar at halaga ng pag-andar sa isang punto x= 1 ay katumbas. Samakatuwid, ang pag-andar ay tuloy-tuloy sa punto x = 1 .

Dot x= 3 . Hanapin ang kaliwang limitasyon sa puntong ito:

Hanapin natin ang limitasyon sa kanang kamay:

Limitasyon sa pag-andar at halaga ng pag-andar sa isang punto x= 3 ay dapat matagpuan sa sangay ng function na kinabibilangan ng puntong ito, iyon ay, ang pangalawang sangay. Natagpuan namin sila:

.

Limitasyon sa pag-andar at halaga ng pag-andar sa isang punto x= 3 ay pantay. Samakatuwid, ang pag-andar ay tuloy-tuloy sa punto x = 3 .

Pangunahing konklusyon: ang function na ito ay tuloy-tuloy sa bawat hangganang punto.

Itatag ang pagpapatuloy ng isang function sa isang punto sa iyong sarili, at pagkatapos ay tingnan ang solusyon

Ang tuluy-tuloy na pagbabago sa isang function ay maaaring tukuyin bilang isang pagbabago na unti-unti, nang walang mga jump, kung saan ang isang maliit na pagbabago sa argument ay humahantong sa isang maliit na pagbabago sa function .

Ilarawan natin ang patuloy na pagbabago ng function na ito gamit ang isang halimbawa.

Hayaang mabitin ang isang load sa isang thread sa itaas ng talahanayan. Sa ilalim ng pagkilos ng load na ito, ang thread ay nakaunat, kaya ang distansya l Ang pag-load mula sa punto ng pagsususpinde ng thread ay isang function ng mass ng load m, ibig sabihin l = f(m) , m≥0 .

Kung bahagyang binago natin ang masa ng pag-load, pagkatapos ay ang distansya l maliit na pagbabago: maliit na pagbabago m tumutugma sa maliliit na pagbabago l. Gayunpaman, kung ang masa ng pagkarga ay malapit sa makunat na lakas ng thread, kung gayon ang isang maliit na pagtaas sa masa ng pagkarga ay maaaring maging sanhi ng pagkasira ng thread: ang distansya l ay biglang tataas at magiging katumbas ng distansya mula sa suspension point hanggang sa table surface. Function Graph l = f(m) ipinapakita sa figure. Sa site, ang graph na ito ay isang tuluy-tuloy (solid) na linya, at sa puntong ito ay naaantala. Ang resulta ay isang graph na binubuo ng dalawang sangay. Sa lahat ng punto maliban sa , ang function l = f(m) ay tuluy-tuloy, at sa isang punto ay mayroon itong discontinuity.

Ang pag-aaral ng isang function para sa pagpapatuloy ay maaaring maging isang independiyenteng gawain at isa sa mga yugto ng kumpletong pag-aaral ng function at ang pagbuo ng graph nito.

Pagpapatuloy ng isang function sa isang pagitan

Hayaan ang function y = f(x) tinukoy sa pagitan ] a, b[ at tuloy-tuloy sa bawat punto ng agwat na ito. Pagkatapos ito ay tinatawag na tuloy-tuloy sa pagitan ] a, b[ . Ang konsepto ng pagpapatuloy ng isang function sa mga pagitan ng anyo ]- ∞ ay parehong tinukoy, b[ , ]a, + ∞[ , ]- ∞, + ∞[ . Ngayon hayaan ang pag-andar y = f(x) tinukoy sa segment [ a, b] . Ang pagkakaiba sa pagitan ng isang agwat at isang segment ay ang mga boundary point ng agwat ay hindi kasama sa agwat, ngunit ang mga boundary point ng segment ay kasama sa segment. Dito dapat nating banggitin ang tinatawag na one-sided continuity: sa punto a, nananatili sa pagitan [ a, b] , makakalapit lang tayo mula sa kanan, at hanggang sa punto b- sa kaliwa lang. Ang function ay tinatawag na tuloy-tuloy sa segment [ a, b] , kung ito ay tuloy-tuloy sa lahat ng panloob na punto ng segment na ito, tuloy-tuloy sa kanan sa punto a at iniwan tuloy-tuloy sa punto b.

Anuman sa mga elementary function ay maaaring magsilbi bilang isang halimbawa ng isang tuluy-tuloy na function. Ang bawat elementary function ay tuloy-tuloy sa anumang segment kung saan ito tinukoy. Halimbawa, ang mga function at tuluy-tuloy sa anumang pagitan [ a, b] , tuloy-tuloy ang function sa segment [ 0 , b] , ang function ay tuloy-tuloy sa anumang segment na hindi naglalaman ng isang punto a = 2 .

Halimbawa 4 Siyasatin ang function para sa pagpapatuloy.

Solusyon. Suriin natin ang unang kondisyon. Ang function ay hindi tinukoy sa mga punto - 3 at 3. Hindi bababa sa isa sa mga kondisyon para sa pagpapatuloy ng function sa buong linya ng numero ay hindi nasiyahan. Samakatuwid, ang function na ito ay tuloy-tuloy sa mga pagitan

Halimbawa 5 Tukuyin kung anong halaga ng parameter a tuloy-tuloy sa kabuuan mga domain function

Solusyon.

Hanapin natin ang kanang-kamay na limitasyon para sa:

.

Ito ay malinaw na ang halaga sa punto x= 2 ay dapat na katumbas palakol :

a = 1,5 .

Halimbawa 6 Tukuyin kung anong mga halaga ng mga parameter a At b tuloy-tuloy sa kabuuan mga domain function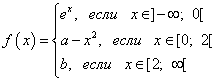

Solusyon.
Hanapin ang kaliwang limitasyon ng function sa punto :

.

Samakatuwid, ang halaga sa punto ay dapat na katumbas ng 1:

Hanapin natin ang left-side function sa puntong :

Malinaw, ang halaga ng function sa punto ay dapat na katumbas ng:

Sagot: ang function ay tuloy-tuloy sa buong domain ng kahulugan para sa a = 1; b = -3 .

Mga pangunahing katangian ng tuluy-tuloy na pag-andar

Ang matematika ay dumating sa konsepto ng isang tuluy-tuloy na pag-andar sa pamamagitan ng pag-aaral, una sa lahat, iba't ibang mga batas ng paggalaw. Ang espasyo at oras ay walang katapusan at ang dependency ay parang mga landas s mula sa panahon t, ipinahayag ng batas s = f(t) , ay nagbibigay ng halimbawa ng tuluy-tuloy mga function f(t). Ang temperatura ng pinainit na tubig ay patuloy ding nagbabago, ito rin ay patuloy na pag-andar ng oras: T = f(t) .

Sa mathematical analysis, ilang mga katangian ang napatunayan na tuluy-tuloy na pag-andar. Ipinakita namin ang pinakamahalaga sa mga katangiang ito.

1. Kung ang isang function na tuluy-tuloy sa isang agwat ay tumatagal sa mga halaga ng iba't ibang mga palatandaan sa mga dulo ng agwat, pagkatapos ay sa isang punto ng segment na ito ay tumatagal ito sa isang halaga na katumbas ng zero. Mas pormal, ang ari-arian na ito ay ibinigay sa isang teorem na kilala bilang ang unang Bolzano-Cauchy theorem.

2. Pag-andar f(x), tuloy-tuloy sa pagitan [ a, b] , kinukuha ang lahat ng mga intermediate na halaga sa pagitan ng mga halaga sa mga endpoint, iyon ay, sa pagitan ng f(a) At f(b). Mas pormal, ang ari-arian na ito ay ibinigay sa isang teorem na kilala bilang pangalawang Bolzano-Cauchy theorem.

Pagpapatuloy ng isang function sa isang punto. Function y = f(x ) ay tinatawag na unpre-

hindi nagpapatuloy sa puntong x 0 kung:

1) ang function na ito ay tinukoy sa ilang kapitbahayan ng punto x 0 ;

2) may limitasyon lim f(x);

→ x0

kung at kung sa puntong ito ang isang infinitesimal increment ng argument ay tumutugma sa isang infinitesimal increment ng function.

Unilateral na pagpapatuloy. Ang function na y \u003d f (x) ay tinatawag na tuloy-tuloy

kaliwa sa puntong x 0 kung ito ay tinukoy sa ilang kalahating pagitan(a ;x 0 ]

at lim f (x )= f (x 0 ) .

x→ x0 − 0

Ang function na y \u003d f (x) ay tinatawag na right-continuous sa puntong x 0 kung ito ay op-

tinukoy sa ilang kalahating pagitan [ x 0 ;a ) at limf (x )= f (x 0 ) .

x→ x0 + 0

Pagpapatuloy ng isang function sa isang set. Ang function na y = f(x) ay tinatawag

tuloy-tuloy sa set X kung ito ay tuloy-tuloy sa bawat punto x ng set na ito. Bukod dito, kung ang function ay tinukoy sa dulo ng isang tiyak na pagitan ng numerical axis, kung gayon ang pagpapatuloy sa puntong ito ay mauunawaan bilang pagpapatuloy sa kanan o kaliwa. Sa partikular, ang function na y = f (x) ay tinatawag na non-

hindi tuloy-tuloy sa segment [ a; b] kung ito

1) tuloy-tuloy sa bawat punto ng pagitan(a ; b);

2) tuloy-tuloy sa kanan sa isang punto a;

3) iniwan tuloy-tuloy sa isang punto b.

Mga function break point. Point x 0 na kabilang sa domain ng kahulugan ng function na y = f (x) , o pagiging boundary point ng domain na ito, ay tinatawag

breakpoint ng function na ito, kung ang f(x) ay hindi tuloy-tuloy sa puntong iyon.

Ang mga breakpoint ay nahahati sa mga breakpoint ng una at pangalawang uri:

1) Kung may mga hangganan lim f (x )= f (x 0 − 0) at

x→ x0 − 0

f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , kung gayon ang x 0 ay tinatawag na discontinuity point.

Sa kasong ito, ang pagtatakda ng f (x 0 )= A , maaari nating baguhin ang function sa puntong x 0

upang ito ay maging tuluy-tuloy muling tukuyin ang function sa pamamagitan ng continuity). Ang pagkakaiba f (x 0 + 0) − f (x 0 − 0) ay tinatawag na function na tumalon sa isang punto x 0 .

Ang pagtalon ng function sa punto ng isang naaalis na discontinuity ay katumbas ng zero.

2) Tinatawag na mga discontinuity point na hindi mga discontinuity point ng unang uri mga discontinuity point ng pangalawang uri. Sa mga discontinuity point ng pangalawang uri, hindi bababa sa isa sa mga one-sided na limitasyon f (x 0 − 0) at f (x 0 + 0) ay wala o walang katapusan.

Mga katangian ng mga function na tuloy-tuloy sa isang punto.

2) Kung ang function na u (x) ay tuloy-tuloy sa puntong x 0, at ang function na f (u) ay tuloy-tuloy

sa puntong u 0 = u (x 0 ) , kung gayon ang kumplikadong function f (u (x )) ay tuloy-tuloy sa puntong x 0 .

3) Ang lahat ng pangunahing elementarya function ( c , x a , a x , loga x , sinx , cosx , tgx , ctgx , secx , cosecx , arcsinx , arccosx , arctgx , arcctgx ) ay tuluy-tuloy sa bawat

hanggang sa punto ng kanilang mga domain ng kahulugan.

Ito ay sumusunod mula sa mga katangian 1)–3) na ang lahat ng elementarya na pag-andar (mga pag-andar na nakuha mula sa mga pangunahing pag-andar ng elementarya sa tulong ng isang may hangganang bilang ng mga pagpapatakbo ng aritmetika at ang pagpapatakbo ng komposisyon) ay tuloy-tuloy din sa bawat punto ng kanilang mga domain ng kahulugan.

Mga katangian ng mga function na tuloy-tuloy sa isang agwat.

1) (teorama tungkol sa mga intermediate na halaga) Hayaang tukuyin ang function na f(x).

on at tuloy-tuloy sa pagitan [ a ; b ] . Pagkatapos ay para sa anumang numerong C na nakapaloob

sa pagitan ng mga numero f (a) at f (b), (f (a)< C < f (b )) найдется хотя бы одна точкаx 0 [ a ;b ] , такая, чтоf (x 0 )= C .

2) (Bolzano–Cauchy theorem

hindi nagpapatuloy sa segment [ a ; b ] at tumatagal sa mga dulo nito ang mga halaga ng iba't ibang mga palatandaan.

Pagkatapos ay mayroong kahit isang punto x 0 [ a ;b ] na ang f (x 0 )= 0 .

3) (1st Teorama ng Weierstrass) Hayaang tukuyin at walang pagbabago ang function na f (x).

hindi tuloy-tuloy sa segment [ a ; b ] . Pagkatapos ang function na ito ay nakatali sa agwat na ito.

4) (ika-2 Teorama ng Weierstrass) Hayaang tukuyin at walang pagbabago ang function na f (x).

f (x 1 )≤ f (x )≤ f (x 2 ) .

Halimbawa 5.17. Gamit ang kahulugan ng continuity, patunayan na ang function na y = 3x 2 + 2x − 5 ay tuloy-tuloy sa isang arbitrary point x 0 sa totoong axis.

Solusyon: 1 paraan: Hayaang ang x 0 ay isang arbitrary na punto sa totoong axis. Ikaw-

una naming kalkulahin ang limitasyon ng function f (x) bilang x → x 0, inilalapat ang mga theorems sa limitasyon ng kabuuan at ang produkto ng mga function:

kahulugan at nangangahulugan ng pagpapatuloy ng itinuturing na function sa punto x 0 .

Kaya, lim y = 0 , na nangangahulugang, sa pamamagitan ng kahulugan, pagpapatuloy

x → 0

function para sa anumang x 0 R .

Halimbawa 5.18. Hanapin ang mga breakpoint ng function na f (x) at tukuyin ang kanilang genus. SA

sa kaso ng isang malulutas na discontinuity, pahabain ang function sa pamamagitan ng continuity:

1) f (x) = 1 − x 2 para sa x< 3;

5x para sa x ≥ 3

2) f (x) \u003d x 2 + 4 x + 3;

x+1

Solusyon: 1) Ang domain ng function na ito ay ang buong numero

kaliwang axis (−∞ ;+∞ ) . Sa mga pagitan (−∞ ;3) ,(3;+∞ ) ang function ay tuloy-tuloy. Ang puwang ay posible lamang sa puntong x = 3 , kung saan nagbabago ang analytical na kahulugan ng function.

Hanapin ang mga one-sided na limitasyon ng function sa tinukoy na punto:

f (3− 0)= lim (1− x 2 )= 1− 9= 8;

x→3 −0

f (3+ 0)= lim 5x = 15.

x →3 +0

Ang f (x ) ay tamang tuloy-tuloy.

2) Ang function ay tuloy-tuloy sa buong axis ng numero, maliban sa punto x = − 1, kung saan hindi ito tinukoy. Binabago namin ang expression para sa f (x) sa pamamagitan ng pagpapalawak ng numerator

Nalaman namin na ang kaliwa at kanang mga limitasyon ng function sa puntong pinag-aaralan ay umiiral, ay may hangganan at katumbas ng bawat isa, samakatuwid x = − 1

ang tuwid na linya y = x + 3 na may "punched out" na punto M (− 1;2) . Para maging pare-pareho ang function

hindi nagpapatuloy, dapat nating ilagay ang f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 .

Kaya, sa pagpapahaba ng f (x ) sa pamamagitan ng continuity sa puntong x = − 1, nakuha namin ang isang function f * (x )= x + 3 na may domain (−∞ ;+∞ ) .

3) Ang function na ito ay tinukoy at tuloy-tuloy para sa lahat x , maliban sa mga puntos

x = 0 ,x = 2 , kung saan nawawala ang denominator ng fraction.

Isaalang-alang ang punto x = 0:

Dahil sa isang sapat na maliit na kapitbahayan ng zero, ang function ay tumatagal lamang

Isaalang-alang ngayon ang punto x = 2:

Ang function ay tumatagal ng mga negatibong halaga malapit sa kaliwa ng isinasaalang-alang

Ang tion ay walang kaliwa o kanan na may hangganan, ibig sabihin. ay nagdurusa ng isang discontinuity ng pangalawang uri sa puntong ito.

Mga gawain para sa malayang solusyon

5.174. Gamit lamang ang kahulugan, patunayan ang pagpapatuloy ng function f ( x ) in

bawat punto x 0 R :

sa puntong x = 0 , ngunit right-continuous sa puntong iyon. I-plot ang function na f (x ) .

Alin sa mga kondisyon ng pagpapatuloy sa mga discontinuity point ng mga function na ito ang nasiyahan at alin ang hindi?

5.179. Tumukoy ng function break point

Alin sa mga kondisyon ng pagpapatuloy sa puntong ito ang natutugunan at alin ang hindi?