4 meravigliosi punti di un triangolo e le loro proprietà. Quattro meravigliosi punti del triangolo

Ci sono i cosiddetti quattro punti notevoli in un triangolo: il punto di intersezione delle mediane. Il punto di intersezione delle bisettrici, il punto di intersezione delle altezze e il punto di intersezione delle bisettrici perpendicolari. Consideriamo ciascuno di essi.

Punto di intersezione delle mediane di un triangolo

Teorema 1

Sull'intersezione delle mediane di un triangolo: Le mediane di un triangolo si intersecano in un punto e dividono il punto di intersezione in un rapporto di $2:1$ partendo dal vertice.

Prova.

Si consideri il triangolo $ABC$, dove $(AA)_1,\ (BB)_1,\ (CC)_1$ è la sua mediana. Poiché le mediane dividono i lati a metà. Considera la linea mediana $A_1B_1$ (Fig. 1).

Figura 1. Mediane di un triangolo

Per il Teorema 1, $AB||A_1B_1$ e $AB=2A_1B_1$, quindi $\angolo ABB_1=\angolo BB_1A_1,\ \angolo BAA_1=\angolo AA_1B_1$. Quindi i triangoli $ABM$ e $A_1B_1M$ sono simili secondo il primo criterio di somiglianza del triangolo. Quindi

Allo stesso modo, è dimostrato che

Il teorema è stato dimostrato.

Punto di intersezione delle bisettrici di un triangolo

Teorema 2

Sull'intersezione delle bisettrici di un triangolo: Le bisettrici di un triangolo si intersecano in un punto.

Prova.

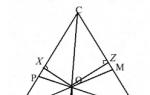
Si consideri il triangolo $ABC$, dove $AM,\ BP,\ CK$ sono le sue bisettrici. Sia il punto $O$ il punto di intersezione delle bisettrici $AM\ e\ BP$. Disegna da questo punto perpendicolare ai lati del triangolo (Fig. 2).

Figura 2. Bisettrici di un triangolo

Teorema 3

Ogni punto della bisettrice di un angolo non espanso è equidistante dai suoi lati.

Per il Teorema 3, abbiamo: $OX=OZ,\ OX=OY$. Quindi $OY=OZ$. Quindi il punto $O$ è equidistante dai lati dell'angolo $ACB$ e giace quindi sulla sua bisettrice $CK$.

Il teorema è stato dimostrato.

Punto di intersezione delle bisettrici perpendicolari di un triangolo

Teorema 4

Le bisettrici perpendicolari dei lati di un triangolo si intersecano in un punto.

Prova.

Sia dato un triangolo $ABC$, $n,\ m,\ p$ le sue bisettrici perpendicolari. Sia il punto $O$ il punto di intersezione delle bisettrici perpendicolari $n\ e\ m$ (Fig. 3).

Figura 3. Bisettrici perpendicolari di un triangolo

Per la dimostrazione abbiamo bisogno del seguente teorema.

Teorema 5

Ogni punto della bisettrice perpendicolare a un segmento è equidistante dalle estremità del segmento dato.

Per il Teorema 3, abbiamo: $OB=OC,\ OB=OA$. Quindi $OA=OC$. Ciò significa che il punto $O$ è equidistante dalle estremità del segmento $AC$ e, quindi, giace sulla sua bisettrice perpendicolare $p$.

Il teorema è stato dimostrato.

Il punto di intersezione delle altitudini del triangolo

Teorema 6

Le altezze di un triangolo o le loro estensioni si intersecano in un punto.

Prova.

Considera il triangolo $ABC$, dove $(AA)_1,\ (BB)_1,\ (CC)_1$ è la sua altezza. Disegna una linea attraverso ciascun vertice del triangolo parallela al lato opposto al vertice. Otteniamo un nuovo triangolo $A_2B_2C_2$ (Fig. 4).

Figura 4. Altezze di un triangolo

Poiché $AC_2BC$ e $B_2ABC$ sono parallelogrammi con un lato comune, allora $AC_2=AB_2$, cioè il punto $A$ è il punto medio del lato $C_2B_2$. Allo stesso modo, otteniamo che il punto $B$ è il punto medio del lato $C_2A_2$ e il punto $C$ è il punto medio del lato $A_2B_2$. Dalla costruzione abbiamo che $(CC)_1\bot A_2B_2,\ (BB)_1\bot A_2C_2,\ (AA)_1\bot C_2B_2$. Quindi $(AA)_1,\ (BB)_1,\ (CC)_1$ sono le bisettrici perpendicolari del triangolo $A_2B_2C_2$. Quindi, per il Teorema 4, abbiamo che le altezze $(AA)_1,\ (BB)_1,\ (CC)_1$ si intersecano in un punto.

In questa lezione esamineremo quattro punti meravigliosi del triangolo. Ci soffermeremo su due di essi in dettaglio, richiameremo le dimostrazioni di importanti teoremi e risolveremo il problema. Le restanti due le ricordiamo e le caratterizziamo.

Soggetto:Ripetizione del corso di geometria della 8° elementare

Lezione: quattro punti notevoli di un triangolo

Un triangolo è, prima di tutto, tre segmenti e tre angoli, quindi le proprietà dei segmenti e degli angoli sono fondamentali.

Viene dato il segmento AB. Ogni segmento ha un centro e attraverso di esso si può tracciare una perpendicolare - lo indichiamo con p. Quindi p è la bisettrice perpendicolare.

Teorema (proprietà di base della bisettrice perpendicolare)

Qualsiasi punto giacente sulla bisettrice perpendicolare è equidistante dalle estremità del segmento.

Prova che

Prova:

Considera i triangoli e (vedi Fig. 1). Sono rettangolari e uguali, perché. hanno una gamba comune OM e le gambe di AO e OB sono uguali per condizione, quindi abbiamo due triangoli rettangoli uguali in due gambe. Ne consegue che anche le ipotenuse dei triangoli sono uguali, cioè da dimostrare.

Riso. uno

Il teorema inverso è vero.

Teorema

Ogni punto equidistante dalle estremità di un segmento giace sulla bisettrice perpendicolare a questo segmento.

Viene dato il segmento AB, la mediana perpendicolare ad esso p, il punto M, equidistante dalle estremità del segmento (vedi Fig. 2).

Dimostrare che il punto M giace sulla bisettrice perpendicolare al segmento.

Riso. 2

Prova:

Consideriamo un triangolo. È isoscele, come per condizione. Considera la mediana del triangolo: il punto O è il punto medio della base AB, OM è la mediana. Secondo la proprietà di un triangolo isoscele, la mediana disegnata alla sua base è sia un'altezza che una bisettrice. Da ciò ne consegue che . Ma anche la retta p è perpendicolare ad AB. Sappiamo che una sola perpendicolare al segmento AB può essere tracciata nel punto O, il che significa che le rette OM e p coincidono, quindi ne segue che il punto M appartiene alla retta p, che doveva essere dimostrata.

Se è necessario descrivere un cerchio attorno a un segmento, questo può essere fatto, e ci sono infiniti di questi cerchi, ma il centro di ciascuno di essi giace sulla bisettrice perpendicolare al segmento.

Si dice che la bisettrice perpendicolare sia il luogo dei punti equidistanti dalle estremità di un segmento.

Il triangolo è composto da tre segmenti. Disegniamo le perpendicolari medie a due di esse e otteniamo il punto O della loro intersezione (vedi Fig. 3).

Il punto O appartiene alla bisettrice perpendicolare al lato BC del triangolo, il che significa che è equidistante dai suoi vertici B e C, indichiamo questa distanza come R:.

Inoltre, il punto O si trova sulla bisettrice perpendicolare al segmento AB, cioè , tuttavia , da qui .

Quindi, il punto O dell'intersezione di due punti medi

Riso. 3

perpendicolari del triangolo è equidistante dai suoi vertici, il che significa che giace anche sulla terza bisettrice perpendicolare.

Abbiamo ripetuto la dimostrazione di un importante teorema.

Le tre bisettrici perpendicolari di un triangolo si intersecano in un punto: il centro del cerchio circoscritto.

Quindi, abbiamo considerato il primo punto notevole di un triangolo: il punto di intersezione delle sue bisettrici perpendicolari.

Passiamo alla proprietà di un angolo arbitrario (vedi Fig. 4).

Dato un angolo, la sua bisettrice AL, punto M giace sulla bisettrice.

Riso. 4

Se il punto M giace sulla bisettrice dell'angolo, allora è equidistante dai lati dell'angolo, cioè le distanze dal punto M ad AC e al BC dei lati dell'angolo sono uguali.

Prova:

Considera triangoli e . Questi sono triangoli rettangoli e sono uguali, perché. hanno un'ipotenusa comune AM, e gli angoli e sono uguali, poiché AL è la bisettrice dell'angolo . Pertanto, i triangoli rettangoli sono uguali in ipotenusa e angolo acuto, quindi ne consegue che , che doveva essere dimostrato. Pertanto, un punto sulla bisettrice di un angolo è equidistante dai lati di quell'angolo.

Il teorema inverso è vero.

Teorema

Se un punto è equidistante dai lati di un angolo non espanso, allora giace sulla sua bisettrice (vedi Fig. 5).

Viene dato un angolo non sviluppato, punto M, tale che la distanza da esso ai lati dell'angolo sia la stessa.

Dimostra che il punto M giace sulla bisettrice dell'angolo.

Riso. 5

Prova:

La distanza da un punto a una retta è la lunghezza della perpendicolare. Disegna dal punto M le perpendicolari MK al lato AB e MP al lato AC.

Considera triangoli e . Questi sono triangoli rettangoli e sono uguali, perché. hanno un'ipotenusa AM comune, le gambe MK e MR sono uguali per condizione. Pertanto, i triangoli rettangoli sono uguali in ipotenusa e gamba. Dall'uguaglianza dei triangoli segue l'uguaglianza degli elementi corrispondenti, angoli uguali giacciono contro gambe uguali, quindi, , quindi, il punto M giace sulla bisettrice dell'angolo dato.

Se è necessario inscrivere un cerchio in un angolo, questo può essere fatto, e ci sono infiniti di questi cerchi, ma i loro centri giacciono sulla bisettrice dell'angolo dato.

Si dice che la bisettrice sia il luogo dei punti equidistanti dai lati di un angolo.

Un triangolo è formato da tre angoli. Costruiamo le bisettrici di due di esse, otteniamo il punto O della loro intersezione (vedi Fig. 6).

Il punto O giace sulla bisettrice dell'angolo, il che significa che è equidistante dai suoi lati AB e BC, indichiamo la distanza come r:. Inoltre, il punto O giace sulla bisettrice dell'angolo , il che significa che è equidistante dai suoi lati AC e BC: , , quindi .

È facile vedere che il punto di intersezione delle bisettrici è equidistante dai lati del terzo angolo, il che significa che giace su

Riso. 6

bisettrice angolare. Pertanto, tutte e tre le bisettrici di un triangolo si intersecano in un punto.

Quindi, abbiamo ricordato la dimostrazione di un altro importante teorema.

Le bisettrici degli angoli di un triangolo si intersecano in un punto: il centro del cerchio inscritto.

Quindi, abbiamo considerato il secondo meraviglioso punto del triangolo: il punto di intersezione delle bisettrici.

Abbiamo esaminato la bisettrice di un angolo e ne abbiamo notato le proprietà importanti: i punti della bisettrice sono equidistanti dai lati dell'angolo, inoltre, i segmenti di tangenti disegnati al cerchio da un punto sono uguali.

Introduciamo alcune notazioni (vedi Fig. 7).

Indichiamo segmenti uguali di tangenti con x, y e z. Il lato BC che giace opposto al vertice A è indicato come a, similmente AC come b, AB come c.

Riso. 7

Problema 1: In un triangolo sono noti il semiperimetro e la lunghezza del lato a. Trova la lunghezza della tangente tracciata dal vertice A - AK, indicato con x.

Ovviamente, il triangolo non è completamente definito e ci sono molti di questi triangoli, ma si scopre che hanno alcuni elementi in comune.

Per problemi in cui stiamo parlando di un cerchio inscritto, possiamo proporre la seguente tecnica di soluzione:

1. Disegna le bisettrici e ottieni il centro del cerchio inscritto.

2. Dal centro O, disegna le perpendicolari ai lati e ottieni i punti di contatto.

3. Segna tangenti uguali.

4. Scrivi la connessione tra i lati del triangolo e le tangenti.

Punto di intersezione delle mediane di un triangolo

Teorema 1

Sull'intersezione delle mediane di un triangolo: Le mediane di un triangolo si intersecano in un punto e dividono il punto di intersezione in un rapporto di $2:1$ partendo dal vertice.

Prova.

Si consideri il triangolo $ABC$, dove $(AA)_1,\ (BB)_1,\ (CC)_1$ è la sua mediana. Poiché le mediane dividono i lati a metà. Considera la linea mediana $A_1B_1$ (Fig. 1).

Figura 1. Mediane di un triangolo

Allo stesso modo, è dimostrato che

Il teorema è stato dimostrato.

Punto di intersezione delle bisettrici di un triangolo

Teorema 2

Sull'intersezione delle bisettrici di un triangolo: Le bisettrici di un triangolo si intersecano in un punto.

Prova.

Figura 2. Bisettrici di un triangolo

Teorema 3

Ogni punto della bisettrice di un angolo non espanso è equidistante dai suoi lati.

Per il Teorema 3, abbiamo: $OX=OZ,\ OX=OY$. Quindi $OY=OZ$. Quindi il punto $O$ è equidistante dai lati dell'angolo $ACB$ e giace quindi sulla sua bisettrice $CK$.

Il teorema è stato dimostrato.

Punto di intersezione delle bisettrici perpendicolari di un triangolo

Teorema 4

Le bisettrici perpendicolari dei lati di un triangolo si intersecano in un punto.

Prova.

Sia dato un triangolo $ABC$, $n,\ m,\ p$ le sue bisettrici perpendicolari. Sia il punto $O$ il punto di intersezione delle bisettrici perpendicolari $n\ e\ m$ (Fig. 3).

Figura 3. Bisettrici perpendicolari di un triangolo

Per la dimostrazione abbiamo bisogno del seguente teorema.

Teorema 5

Ogni punto della bisettrice perpendicolare a un segmento è equidistante dalle estremità del segmento dato.

Il teorema è stato dimostrato.

Il punto di intersezione delle altitudini del triangolo

Teorema 6

Le altezze di un triangolo o le loro estensioni si intersecano in un punto.

Prova.

Figura 4. Altezze di un triangolo

Soggetto:Ripetizione del corso di geometria della 8° elementare

Lezione: quattro punti notevoli di un triangolo

Un triangolo è, prima di tutto, tre segmenti e tre angoli, quindi le proprietà dei segmenti e degli angoli sono fondamentali.

Viene dato il segmento AB. Ogni segmento ha un centro e attraverso di esso si può tracciare una perpendicolare - lo indichiamo con p. Quindi p è la bisettrice perpendicolare.

Teorema (proprietà di base della bisettrice perpendicolare)

Qualsiasi punto giacente sulla bisettrice perpendicolare è equidistante dalle estremità del segmento.

Prova che

Prova:

Riso. uno

Il teorema inverso è vero.

Teorema

Ogni punto equidistante dalle estremità di un segmento giace sulla bisettrice perpendicolare a questo segmento.

Viene dato il segmento AB, la mediana perpendicolare ad esso p, il punto M, equidistante dalle estremità del segmento (vedi Fig. 2).

Dimostrare che il punto M giace sulla bisettrice perpendicolare al segmento.

Riso. 2

Prova:

Si dice che la bisettrice perpendicolare sia il luogo dei punti equidistanti dalle estremità di un segmento.

Il triangolo è composto da tre segmenti. Disegniamo le perpendicolari medie a due di esse e otteniamo il punto O della loro intersezione (vedi Fig. 3).

Il punto O appartiene alla bisettrice perpendicolare al lato BC del triangolo, il che significa che è equidistante dai suoi vertici B e C, indichiamo questa distanza come R:.

Inoltre, il punto O si trova sulla bisettrice perpendicolare al segmento AB, cioè , tuttavia , da qui .

Quindi, il punto O dell'intersezione di due punti medi

Riso. 3

perpendicolari del triangolo è equidistante dai suoi vertici, il che significa che giace anche sulla terza bisettrice perpendicolare.

Abbiamo ripetuto la dimostrazione di un importante teorema.

Le tre bisettrici perpendicolari di un triangolo si intersecano in un punto: il centro del cerchio circoscritto.

Quindi, abbiamo considerato il primo punto notevole di un triangolo: il punto di intersezione delle sue bisettrici perpendicolari.

Passiamo alla proprietà di un angolo arbitrario (vedi Fig. 4).

Dato un angolo, la sua bisettrice AL, punto M giace sulla bisettrice.

Riso. 4

Se il punto M giace sulla bisettrice dell'angolo, allora è equidistante dai lati dell'angolo, cioè le distanze dal punto M ad AC e al BC dei lati dell'angolo sono uguali.

Prova:

Il teorema inverso è vero.

Teorema

Se un punto è equidistante dai lati di un angolo non espanso, allora giace sulla sua bisettrice (vedi Fig. 5).

Viene dato un angolo non sviluppato, punto M, tale che la distanza da esso ai lati dell'angolo sia la stessa.

Dimostra che il punto M giace sulla bisettrice dell'angolo.

Riso. 5

Prova:

La distanza da un punto a una retta è la lunghezza della perpendicolare. Disegna dal punto M le perpendicolari MK al lato AB e MP al lato AC.

Se è necessario inscrivere un cerchio in un angolo, questo può essere fatto, e ci sono infiniti di questi cerchi, ma i loro centri giacciono sulla bisettrice dell'angolo dato.

Si dice che la bisettrice sia il luogo dei punti equidistanti dai lati di un angolo.

Un triangolo è formato da tre angoli. Costruiamo le bisettrici di due di esse, otteniamo il punto O della loro intersezione (vedi Fig. 6).

È facile vedere che il punto di intersezione delle bisettrici è equidistante dai lati del terzo angolo, il che significa che giace su

Riso. 6

bisettrice angolare. Pertanto, tutte e tre le bisettrici di un triangolo si intersecano in un punto.

Quindi, abbiamo ricordato la dimostrazione di un altro importante teorema.

Le bisettrici degli angoli di un triangolo si intersecano in un punto: il centro del cerchio inscritto.

Quindi, abbiamo considerato il secondo meraviglioso punto del triangolo: il punto di intersezione delle bisettrici.

Introduciamo alcune notazioni (vedi Fig. 7).

Indichiamo segmenti uguali di tangenti con x, y e z. Il lato BC che giace opposto al vertice A è indicato come a, similmente AC come b, AB come c.

Riso. 7

Problema 1: In un triangolo sono noti il semiperimetro e la lunghezza del lato a. Trova la lunghezza della tangente tracciata dal vertice A - AK, indicato con x.

Ovviamente, il triangolo non è completamente definito e ci sono molti di questi triangoli, ma si scopre che hanno alcuni elementi in comune.

Per problemi in cui stiamo parlando di un cerchio inscritto, possiamo proporre la seguente tecnica di soluzione:

1. Disegna le bisettrici e ottieni il centro del cerchio inscritto.

2. Dal centro O, disegna le perpendicolari ai lati e ottieni i punti di contatto.

3. Segna tangenti uguali.

4. Scrivi la connessione tra i lati del triangolo e le tangenti.

introduzione

Gli oggetti del mondo che ci circonda hanno determinate proprietà, che sono studiate da varie scienze.

La geometria è una branca della matematica che considera le varie forme e le loro proprietà, le sue radici risalgono a un lontano passato.

Nel quarto libro degli "Inizi", Euclide risolve il problema: "Iscrivi un cerchio in un dato triangolo". Dalla soluzione consegue che le tre bisettrici degli angoli interni di un triangolo si intersecano in un punto: il centro del cerchio inscritto. Dalla soluzione di un altro problema di Euclide, ne consegue che le perpendicolari restaurate ai lati del triangolo nei loro punti medi si intersecano anche in un punto: il centro del cerchio circoscritto. I "Principi" non dicono che le tre altezze di un triangolo si intersecano in un punto, detto ortocentro (la parola greca "orthos" significa "diritto", "corretto"). Questa proposta era, tuttavia, nota ad Archimede. Il quarto punto singolare del triangolo è il punto di intersezione delle mediane. Archimede ha dimostrato che è il baricentro (baricentro) del triangolo.

Ai quattro punti di cui sopra è stata prestata particolare attenzione e dal XVIII secolo sono stati chiamati punti "notevole" o "speciali" del triangolo. Lo studio delle proprietà di un triangolo associato a questi e altri punti è servito come inizio per la creazione di un nuovo ramo della matematica elementare: la "geometria di un triangolo" o la "nuova geometria di un triangolo", uno dei fondatori di cui era Leonhard Euler.

Nel 1765 Eulero dimostrò che in ogni triangolo l'ortocentro, il baricentro e il centro della circonferenza circoscritta giacciono sulla stessa retta, poi chiamata "linea di Eulero". Negli anni venti del XIX secolo, i matematici francesi J. Poncelet, Ch. Brianchon e altri stabilirono indipendentemente il seguente teorema: le basi delle mediane, le basi delle altezze e i punti medi dei segmenti delle altezze che collegano l'ortocentro con i vertici del triangolo giacciono sullo stesso cerchio. Questo cerchio è chiamato il "cerchio di nove punte", o il "cerchio di Feuerbach", o il "cerchio di Eulero". K. Feuerbach stabilì che il centro di questo cerchio si trova sulla linea di Eulero.

“Penso che non abbiamo mai vissuto in un periodo così geometrico fino ad ora. Tutto intorno è geometria. Queste parole, pronunciate dal grande architetto francese Le Corbusier all'inizio del XX secolo, caratterizzano molto accuratamente il nostro tempo. Il mondo in cui viviamo è pieno di geometrie di case e strade, montagne e campi, creazioni della natura e dell'uomo.

Ci interessavano i cosiddetti "punti meravigliosi del triangolo".

Dopo aver letto la letteratura su questo argomento, ci siamo fissati le definizioni e le proprietà dei punti notevoli del triangolo. Ma il nostro lavoro non è finito qui e abbiamo voluto esplorare questi punti noi stessi.

Così obbiettivo dato lavoro - lo studio di alcuni meravigliosi punti e linee del triangolo, l'applicazione delle conoscenze acquisite alla risoluzione di problemi. Nel processo di raggiungimento di questo obiettivo si possono distinguere le seguenti fasi:

Selezione e studio di materiale didattico da varie fonti di informazione, letteratura;

Lo studio delle proprietà di base dei punti e delle rette notevoli del triangolo;

Generalizzazione di queste proprietà e dimostrazione dei teoremi necessari;

Risolvere problemi relativi ai punti notevoli del triangolo.

Capitoloio. Meravigliosi punti e linee triangolari

1.1 Punto di intersezione delle perpendicolari medie ai lati di un triangolo

La bisettrice perpendicolare è una retta passante per il punto medio di un segmento, perpendicolare ad esso. Conosciamo già il teorema che caratterizza la proprietà della bisettrice perpendicolare: ogni punto della bisettrice perpendicolare al segmento è equidistante dalle sue estremità e viceversa, se il punto è equidistante dalle estremità del segmento, allora giace sulla bisettrice perpendicolare.

Il poligono è chiamato inscritto in un cerchio se tutti i suoi vertici appartengono al cerchio. Il cerchio è detto circoscritto vicino al poligono.

Un cerchio può essere circoscritto attorno a qualsiasi triangolo. Il suo centro è il punto di intersezione delle perpendicolari mediali ai lati del triangolo.

Sia il punto O il punto di intersezione delle bisettrici perpendicolari ai lati del triangolo AB e BC.

Conclusione: Quindi, se il punto O è il punto di intersezione delle perpendicolari medie ai lati del triangolo, allora OA = OS = OB, cioè il punto O è equidistante da tutti i vertici del triangolo ABC, il che significa che è il centro del cerchio circoscritto.


ad angolo acuto	ottuso	rettangolare

Conseguenze

sin γ \u003d c / 2R \u003d c / sin γ \u003d 2R.

È dimostrato allo stesso modo un/ peccato α =2R, b/peccato β =2R.

Così:

Questa proprietà è chiamata teorema seno.

In matematica capita spesso che oggetti definiti in modi molto diversi risultino uguali.

Esempio. Siano A1, B1, C1 i punti medi dei lati ∆ABS BC, AC, AB, rispettivamente. Mostra che i cerchi circoscritti ai triangoli AB1C1, A1B1C, A1BC1 si intersecano in un punto. Inoltre, questo punto è il centro della circonferenza circoscritta attorno a ∆ABS.

Considera il segmento AO e costruisci un cerchio su questo segmento, come su un diametro. I punti C1 e B1 cadono su questo cerchio, perché sono vertici di angoli retti basati su AO. I punti A, C1, B1 giacciono su un cerchio = questo cerchio è circoscritto a ∆AB1C1.

Allo stesso modo, disegneremo un segmento BO e costruiremo un cerchio su questo segmento, come su un diametro. Questo sarà un cerchio circoscritto a ∆BC1 A1.

Disegniamo un segmento CO e costruiamo un cerchio su questo segmento, come su un diametro. Questo sarà il cerchio circoscritto

Questi tre cerchi passano per il punto O - il centro del cerchio circoscritto a ∆ABC.

Generalizzazione. Se si prendono punti arbitrari A 1 , B 1 , C 1 ai lati ∆ABC AC, BC, AC, allora i cerchi circoscritti ai triangoli AB 1 C 1 , A 1 B 1 C, A 1 BC 1 si intersecano in un punto .

1.2 Punto di intersezione delle bisettrici di un triangolo

Vale anche l'affermazione inversa: se un punto è equidistante dai lati di un angolo, allora giace sulla sua bisettrice.

È utile segnare le metà di un angolo con le stesse lettere:

OAF=OAD= α, OBD=OBE= β, OCE=OCF= γ.

Sia il punto O il punto di intersezione delle bisettrici degli angoli A e B. Per la proprietà di un punto giacente sulla bisettrice dell'angolo A, OF=OD=r. Per la proprietà di un punto giacente sulla bisettrice dell'angolo B, OE=OD=r. Quindi, OE=OD= OF=r= punto O è equidistante da tutti i lati del triangolo ABC, cioè O è il centro del cerchio inscritto. (Il punto O è l'unico).

Conclusione: Quindi, se il punto O è il punto di intersezione delle bisettrici degli angoli del triangolo, allora OE=OD= OF=r, cioè il punto O è equidistante da tutti i lati del triangolo ABC, il che significa che è il centro del cerchio inscritto. Il punto O - l'intersezione delle bisettrici degli angoli del triangolo è un punto meraviglioso del triangolo.

Conseguenze:

Dall'uguaglianza dei triangoli AOF e AOD (Figura 1) lungo l'ipotenusa e l'angolo acuto, segue che AF = ANNO DOMINI . Dall'uguaglianza dei triangoli OBD e OBE ne consegue che BD = ESSERE , Dall'uguaglianza dei triangoli COE e COF segue che Insieme a F = CE . Pertanto, i segmenti di tangenti disegnati al cerchio da un punto sono uguali.

AF=AD= z, BD=BE= y, СF=CE= X

a=x+y (1), b= x+z (2), c= x+y (3).

+ (2) – (3), quindi otteniamo: a+b-c=X+ y+ X+ z- z- y = a+b-c= 2X =

x=( b + c - a)/2

Allo stesso modo: (1) + (3) - (2), otteniamo: y = (a + c -b)/2.

Allo stesso modo: (2) + (3) - (1), otteniamo: z= (un +b - c)/2.

La bisettrice dell'angolo di un triangolo divide il lato opposto in segmenti proporzionali ai lati adiacenti.

1.3 Punto di intersezione delle mediane di un triangolo (centroide)

Prova 1. Siano A 1 , B 1 e C 1 rispettivamente i punti medi dei lati BC, CA e AB del triangolo ABC (Fig. 4).

Sia G il punto di intersezione di due mediane AA 1 e BB 1 . Dimostriamo innanzitutto che AG:GA 1 = BG:GB 1 = 2.

Per fare ciò, prendi i punti medi P e Q dei segmenti AG e BG. Secondo il teorema della linea mediana del triangolo, i segmenti B 1 A 1 e PQ sono uguali alla metà del lato AB e sono ad esso paralleli. Pertanto, il quadrilatero A 1 B 1 è un parallelogramma PQ. Quindi il punto di intersezione G delle sue diagonali PA 1 e QB 1 le divide in due. Pertanto, i punti P e G dividono la mediana di AA 1 in tre parti uguali, ei punti Q e G dividono anche la mediana di BB 1 in tre parti uguali. Quindi, il punto G dell'intersezione delle due mediane del triangolo divide ciascuna di esse in un rapporto di 2:1, contando dall'alto.

Si chiama il punto di intersezione delle mediane di un triangolo baricentro o centro di gravità triangolo. Questo nome è dovuto al fatto che è in questo punto che si trova il baricentro di una piastra triangolare omogenea.

1.4 Punto di intersezione delle altezze del triangolo (ortocentro)

1.5 Punto Torricelli

Il percorso indicato è il triangolo ABC. Il punto Torricelli di questo triangolo è un tale punto O, dal quale i lati di questo triangolo sono visibili con un angolo di 120°, cioè gli angoli AOB, AOC e BOC sono 120°.

Dimostriamo che se tutti gli angoli del triangolo sono minori di 120°, allora esiste il punto di Torricelli.

Sul lato AB del triangolo ABC, costruiamo un triangolo equilatero ABC "(Fig. 6, a), e descriviamo un cerchio attorno ad esso. Il segmento AB sottende l'arco di questo cerchio con un valore di 120 °. Pertanto, il i punti di questo arco, diversi da A e B, hanno la proprietà che il segmento AB sia visibile da essi con un angolo di 120°. Allo stesso modo, sul lato AC del triangolo ABC, costruiamo un triangolo equilatero ACB "(Fig. 6, a) e descrivere un cerchio attorno ad esso. I punti dell'arco corrispondente, diversi da A e C, hanno la proprietà che il segmento AC sia visibile da essi con un angolo di 120°. Nel caso in cui gli angoli del triangolo siano minori di 120°, questi archi si intersecano in un punto interno O. In questo caso, ∟AOB = 120°, ∟AOC = 120°. Pertanto, ∟BOC = 120°. Pertanto, il punto O è quello desiderato.

Nel caso in cui uno degli angoli del triangolo, ad esempio ABC, sia uguale a 120°, il punto di intersezione degli archi dei cerchi sarà il punto B (Fig. 6, b). In questo caso il punto Torricelli non esiste, poiché è impossibile parlare degli angoli ai quali i lati AB e BC sono visibili da questo punto.

Nel caso in cui uno degli angoli del triangolo, ad esempio ABC, sia maggiore di 120° (Fig. 6, c), gli archi di cerchio corrispondenti non si intersecano e anche il punto di Torricelli non esiste.

Relativo al punto di Torricelli è il problema di Fermat (che considereremo nel Capitolo II) di trovare il punto da cui la somma delle distanze da cui a tre punti dati è la più piccola.

1.6 Cerchio di nove punti

Infatti, A 3 B 2 è la linea mediana del triangolo AHC e, di conseguenza, A 3 B 2 || CC1. B 2 A 2 è la linea mediana del triangolo ABC e, quindi, B 2 A 2 || AB. Poiché CC 1 ┴ AB, allora A 3 B 2 A 2 = 90°. Allo stesso modo, A 3 C 2 A 2 = 90°. Quindi i punti A 2 , B 2 , C 2 , A 3 giacciono sullo stesso cerchio di diametro A 2 A 3 . Poiché AA 1 ┴BC, anche il punto A 1 appartiene a questo cerchio. Pertanto, i punti A 1 e A 3 giacciono sulla circonferenza del triangolo A2B2C2. Allo stesso modo, si mostra che i punti B 1 e B 3 , C 1 e C 3 giacciono su questo cerchio. Quindi tutti e nove i punti giacciono sullo stesso cerchio.

In questo caso, il centro del cerchio di nove punti si trova nel mezzo tra il centro dell'intersezione delle altezze e il centro del cerchio circoscritto. Sia infatti nel triangolo ABC (fig. 9) il punto O il centro del cerchio circoscritto; G è il punto di intersezione delle mediane. H punto di intersezione delle altezze. È necessario dimostrare che i punti O, G, H giacciono sulla stessa retta e il centro del cerchio di nove punti N divide a metà il segmento OH.

Si consideri un'omoteità centrata in G e con coefficiente -0,5. I vertici A, B, C del triangolo ABC andranno rispettivamente ai punti A 2 , B 2 , C 2. Le altezze del triangolo ABC andranno alle altezze del triangolo A 2 B 2 C 2 e, di conseguenza, il punto H andrà al punto O. Pertanto, i punti O, G, H giaceranno su una retta.

Mostriamo che il punto medio N del segmento OH è il centro del cerchio di nove punti. Infatti, C 1 C 2 è la corda di nove punti del cerchio. Pertanto, la bisettrice perpendicolare a questa corda è il diametro e interseca OH nel punto medio di N. Allo stesso modo, la bisettrice perpendicolare alla corda B 1 B 2 è il diametro e interseca OH nello stesso punto N. Quindi, N è il centro del cerchio di nove punti. QED

Sia infatti P un punto arbitrario giacente sulla circonferenza del triangolo ABC; D, E, F sono le basi delle perpendicolari cadute dal punto P ai lati del triangolo (Fig. 10). Mostriamo che i punti D, E, F giacciono sulla stessa retta.

Si noti che se AP passa per il centro del cerchio, i punti D ed E coincidono con i vertici B e C. Altrimenti, uno degli angoli ABP o ACP è acuto e l'altro è ottuso. Ne consegue che i punti D ed E saranno posti su lati diversi della retta BC, e per provare che i punti D, E ed F giacciono sulla stessa retta basta verificare che ∟CEF =∟ LETTO.

Descriviamo un cerchio di diametro CP. Poiché ∟CFP = ∟CEP = 90°, i punti E ed F giacciono su questo cerchio. Pertanto, ∟CEF =∟CPF come angoli inscritti basati su un arco circolare. Inoltre, ∟CPF = 90°- ∟PCF = 90°- ∟DBP = ∟BPD. Descriviamo un cerchio di diametro BP. Poiché ∟BEP = ∟BDP = 90°, i punti F e D giacciono su questo cerchio. Pertanto, ∟BPD = ∟BED. Pertanto, otteniamo infine che ∟CEF =∟BED. Quindi i punti D, E, F giacciono sulla stessa retta.

CapitoloIIRisoluzione dei problemi

Iniziamo con i problemi relativi alla posizione delle bisettrici, delle mediane e delle altezze di un triangolo. La loro soluzione, da un lato, consente di ricordare il materiale trattato in precedenza e, dall'altro, sviluppa le rappresentazioni geometriche necessarie, si prepara a risolvere problemi più complessi.

Compito 1. Agli angoli A e B del triangolo ABC (∟A

Decisione. Sia CD l'altezza, CE la bisettrice, quindi

∟BCD = 90° - ∟B, ∟BCE = (180° - ∟A - ∟B):2.

Pertanto, ∟DCE =.

Decisione. Sia O il punto di intersezione delle bisettrici del triangolo ABC (Fig. 1). Sfruttiamo il fatto che un angolo più grande si trova di fronte al lato più grande del triangolo. Se AB BC, allora ∟A

Decisione. Sia O il punto di intersezione delle altezze del triangolo ABC (Fig. 2). Se AC ∟B. Un cerchio di diametro BC passerà per i punti F e G. Considerando che la minore delle due corde è quella su cui poggia l'angolo inscritto minore, otteniamo che CG

Prova. Ai lati AC e BC del triangolo ABC, come sui diametri, costruiamo cerchi. I punti A 1 , B 1 , C 1 appartengono a questi cerchi. Pertanto, ∟B 1 C 1 C = ∟B 1 BC, come angoli basati sullo stesso arco di cerchio. ∟B 1 BC = ∟CAA 1 come angoli con lati tra loro perpendicolari. ∟CAA 1 = ∟CC 1 A 1 come angoli basati sullo stesso arco di cerchio. Pertanto, ∟B 1 C 1 C = ∟CC 1 A 1 , cioè CC 1 è la bisettrice dell'angolo B 1 C 1 A 1 . Allo stesso modo, si mostra che AA 1 e BB 1 sono bisettrici degli angoli B 1 A 1 C 1 e A 1 B 1 C 1 .

Il triangolo considerato, i cui vertici sono le basi delle altezze di un dato triangolo acuto, dà una risposta ad uno dei classici problemi estremi.

Decisione. Sia ABC un dato triangolo acuto. Ai suoi lati è necessario trovare tali punti A 1 , B 1 , C 1 per i quali il perimetro del triangolo A 1 B 1 C 1 sarebbe il più piccolo (Fig. 4).

Fissiamo prima il punto C 1 e cerchiamo i punti A 1 e B 1 per i quali il perimetro del triangolo A 1 B 1 C 1 è il più piccolo (per la posizione data del punto C 1).

Per fare ciò, si considerino i punti D ed E simmetrici al punto C 1 rispetto alle linee AC e BC. Quindi B 1 C 1 \u003d B 1 D, A 1 C 1 \u003d A 1 E e, quindi, il perimetro del triangolo A 1 B 1 C 1 sarà uguale alla lunghezza della polilinea DB 1 A 1 E. È chiaro che la lunghezza di questa polilinea è la più piccola se i punti B 1 , A 1 giacciono sulla linea DE.

Ora cambieremo la posizione del punto C 1 e cercheremo una posizione tale in cui il perimetro del triangolo corrispondente A 1 B 1 C 1 sia il più piccolo.

Poiché il punto D è simmetrico a C 1 rispetto ad AC, allora CD = CC 1 e ACD=ACC 1 . Allo stesso modo, CE=CC 1 e BCE=BCC 1 . Pertanto, il triangolo CDE è isoscele. Il suo lato è uguale a CC 1 . La base DE è uguale al perimetro P triangolo A 1 B 1 C 1 . L'angolo DCE è uguale al doppio dell'angolo ACB del triangolo ABC e, quindi, non dipende dalla posizione del punto C 1 .

In un triangolo isoscele con un dato angolo all'apice, più piccola è la base, più piccolo è il lato. Pertanto, il valore più piccolo del perimetro P si ottiene nel caso del valore più piccolo di CC 1 . Questo valore viene preso se CC 1 è l'altezza del triangolo ABC. Pertanto, il punto richiesto C 1 sul lato AB è la base dell'altezza ricavata dall'alto C.

Si noti che potremmo prima fissare non il punto C 1 , ma il punto A 1 o il punto B 1 e otterremmo che A 1 e B 1 sono le basi delle corrispondenti altezze del triangolo ABC.

Da ciò segue che il triangolo desiderato, il perimetro più piccolo, inscritto in un dato triangolo ad angolo acuto ABC è un triangolo i cui vertici sono le basi delle altezze del triangolo ABC.

Decisione. Dimostriamo che se gli angoli del triangolo sono minori di 120°, allora il punto desiderato nel problema di Steiner è il punto di Torricelli.

Ruotiamo il triangolo ABC attorno al vertice C di un angolo di 60°, fig. 7. Ottieni il triangolo A'B'C. Prendi un punto arbitrario O nel triangolo ABC. Quando si gira, andrà a un certo punto O'. Il triangolo OO'C è equilatero poiché CO = CO' e ∟OCO' = 60°, quindi OC = OO'. Pertanto, la somma delle lunghezze di OA + OB + OC sarà uguale alla lunghezza della polilinea AO + OO' + O'B'. È chiaro che la lunghezza di questa polilinea assume il valore minimo se i punti A, O, O', B' giacciono sulla stessa retta. Se O è un punto Torricelli, allora lo è. Infatti, ∟AOC = 120°, ∟COO" = 60°. Pertanto, i punti A, O, O' giacciono sulla stessa retta. Allo stesso modo, ∟CO'O = 60°, ∟CO"B" = 120° Quindi i punti O, O', B' giacciono sulla stessa retta, il che significa che tutti i punti A, O, O', B' giacciono sulla stessa retta.

Conclusione

La geometria di un triangolo, insieme ad altre sezioni di matematica elementare, permette di sentire la bellezza della matematica in generale e può diventare per qualcuno l'inizio del percorso verso la "grande scienza".

La geometria è una scienza straordinaria. La sua storia abbraccia più di un millennio, ma ogni incontro con lei è in grado di conferire e arricchire (sia l'allievo che l'insegnante) l'emozionante novità di una piccola scoperta, la sorprendente gioia della creatività. In effetti, qualsiasi problema di geometria elementare è, in sostanza, un teorema, e la sua soluzione è una modesta (e talvolta enorme) vittoria matematica.

Storicamente, la geometria è iniziata con un triangolo, quindi per due millenni e mezzo il triangolo è stato un simbolo della geometria. Solo allora la geometria della scuola può diventare interessante e significativa, solo allora può diventare una vera e propria geometria, quando in essa appare uno studio profondo e completo del triangolo. Sorprendentemente, il triangolo, nonostante la sua apparente semplicità, è un oggetto di studio inesauribile: nessuno, nemmeno ai nostri giorni, osa dire di aver studiato e di conoscere tutte le proprietà di un triangolo.

In questo lavoro sono state considerate le proprietà delle bisettrici, delle mediane, delle bisettrici perpendicolari e delle altezze di un triangolo, è stato ampliato il numero di punti e linee notevoli di un triangolo, sono stati formulati e dimostrati teoremi. Sono stati risolti numerosi problemi sull'applicazione di questi teoremi.

Il materiale presentato può essere utilizzato sia nelle lezioni di base che in classi opzionali, nonché in preparazione per i test centralizzati e le olimpiadi di matematica.

Bibliografia

Berger M. Geometry in due volumi - M: Mir, 1984.

Kiselev AP Geometria elementare. – M.: Illuminismo, 1980.

Kokseter GS, Greitzer SL Nuovi incontri con la geometria. – M.: Nauka, 1978.

Latotin LA, Chebotaravskiy BD Matematica 9. - Minsk: Narodnaya Asveta, 2014.

Prasolov V.V. Problemi di planimetria. - M.: Nauka, 1986. - Parte 1.

Scanavi M. I. Matematica. Problemi con soluzioni. - Rostov sul Don: Phoenix, 1998.

Sharygin I.F. Problemi di geometria: Planimetria. – M.: Nauka, 1986.