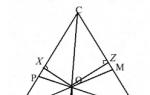
The angle between the height of the median of a right triangle. Task

Note . AT this lesson problems in geometry about the median of a triangle are outlined. If you need to solve a problem in geometry, which is not here - write about it in the forum. Almost certainly the course will be supplemented.

Task

.
Decision.
First, let's build a right triangle to a rectangle.

• The sum of the angles of a triangle is 180 degrees
• The diagonals of the rectangle at the point of intersection are bisected
• The diagonals of a rectangle are equal

Since angle CAB = 20°, then angle ABC = 180 - 90 - 20 = 70°

Triangle COA is isosceles because its sides are half of the rectangle's diagonals. From where ∠OCA = ∠OAC = 20º

Since triangle BKC is a right triangle, angle BCK = 180 - 90 - 70 = 20°

Since angle BCA is a right angle, its degree measure is equal to the sum of the degree measures of angles BCK, KCO and OCA. Where:
20° + 20° + ∠KCO = 90°
∠KCO = 50°

Answer: Angle between the median and the bisector of the given right triangle equals 50 degrees.

Medians of a right triangle

Note . In this lesson, we set out problems in geometry about the median of a triangle. If you need to solve a problem in geometry, which is not here - write about it in the forum. Almost certainly the course will be expanded.

Task. The medians of a right triangle drawn to the legs are 3 cm and 4 cm, respectively. Find the hypotenuse of the triangle

Decision

Let's denote the lengths of the legs AC and BC as 2x and 2y. Then, by the Pythagorean theorem
AC 2 + CD 2 = AD 2

Since AC \u003d 2x, CD \u003d y (since the median divides the leg into two equal parts), then
4x2 + y2 = 9

Simultaneously,
EC 2 + BC 2 = BE 2

Since EC \u003d x (the median bisects the leg), BC \u003d 2y, then
x2 + 4y2 = 16

Let's solve the resulting system of equations.
Let's add both equations.
5x2 + 5y2 = 25
5(x2 + y2) = 25
x2 + y2 = 5

According to the Pythagorean theorem
AC 2 + BC 2 = AB 2
i.e
4x2 + 4y2 = AB2
4 (x 2 + y 2) = AB 2
substitute the values ​​x 2 + y 2 = 5
AB 2 = 20
AB = √20 = 2√5

Answer: the length of the hypotenuse is 2√5

similarity of triangles

This chapter presents solutions to problems in geometry on the topic "similarity of triangles".

Triangles have three similarities.

The first sign of the similarity of triangles

If two angles of one triangle are respectively equal to two angles of another triangle, then such triangles are similar.

Comment . Accordingly, since the sum of all angles of a triangle is 180 degrees, then the same can be said about the third angle of each of these triangles..

Note. In this lesson, we set out problems in geometry about the median of a triangle. If you need to solve a problem in geometry, which is not here - write about it in the forum. Almost certainly the course will be supplemented.

Task. Find the angle between height and median of a right triangle

First, let's build a right triangle to a rectangle.

As a result of the additional construction, the legs of a right-angled triangle are simultaneously the sides of the rectangle, and the hypotenuse is its diagonal.

• The sum of the angles of a triangle is 180 degrees
• The diagonals of the rectangle at the point of intersection are bisected
• The diagonals of a rectangle are equal

The value of one of the angles of the triangle is specified in the condition of the problem. Since the triangle is right-angled by the condition, we can find the value of the third angle, knowing that the sum of the angles of the triangle is 180 degrees.

Since angle CAB = 20°, then angle ABC = 180 - 90 - 20 = 70°
Thus, we have found the degree measure of angle B in triangle ABC

Consider the triangle COA. It is isosceles, since its sides are half the diagonals of the rectangle. This follows from the properties of the rectangle. Since the diagonals of the rectangle are equal, and at the point of intersection they are divided in half, then the halves of equal segments will also be equal to each other. Since in an isosceles triangle the angles at the base are equal, then:
∠OCA = ∠OAC = 20º

Consider triangle BKC. CK is the height triangle ABC drawn to the hypotenuse. So the angle BKC is right, that is, it is equal to 90 degrees, and the triangle BKC itself is right-angled. Since triangle BKC is a right triangle, angle BCK = 180 - 90 - 70 = 20°. (This follows from the fact that the sum of the angles of a triangle is 180 degrees, the angle BKC is a right angle, and we found the value of angle B earlier)

Since the angle BCA is a right angle, its degree measure is equal to 90 degrees and, at the same time, is equal to the sum of the degree measures of its constituent angles: BCK, KCO and OCA.
We just found the BCK angle value, it is 20 degrees, we also found the OCA angle value earlier and it is also 20 degrees.
Where:
20° + 20° + ∠KCO = 90°
∠KCO = 50°

Answer: The angle between the median and the bisector of a given right triangle is 50 degrees.

We will talk about problems for solving a right-angled triangle. These tasks are not related to finding the sides, sine, cosine, tangent or cotangent of angles, such are we.

First, the basic theory about triangles for those who have forgotten it, and for everyone who wants to repeat it 😉

If one of the angles of a triangle is right (equal to 90°), then the triangle is called rectangular. The two sides forming a right angle are called legs, and the opposite side right angle, is called the hypotenuse (Figure 1).

If all angles of a triangle are acute, then the triangle is called acute-angled(Figure 2).

If one of the angles of a triangle is obtuse (greater than 90°), then the triangle is called obtuse(Figure 3).

An equilateral triangle is one in which all three sides are equal. AT equilateral triangle all angles are 60°, and the centers of the inscribed and circumscribed circles coincide (Figure 4).

An isosceles triangle is one in which two sides are equal. These sides are called the sides, the third side is called the base. In an isosceles triangle, the angles at the base are equal (Figure 5).

A triangle is called versatile if the lengths of three sides are pairwise different (Figure 6).

Triangle median

median a triangle drawn from a given vertex is called a segment connecting this vertex with the midpoint of the opposite side (the base of the median). All three medians of a triangle intersect at one point. This intersection divides each median 1:2 from the base of the median (this fact should be remembered).

triangle height

Height a triangle drawn from a given vertex is called a perpendicular dropped from this vertex to the opposite side or its continuation.

Bisector of a triangle

bisectorA triangle drawn from a given vertex is called a segment connecting this vertex to a point on the opposite side and dividing the angle at the given vertex in half. The bisectors of a triangle intersect at one point, and this point coincides with the center of the inscribed circle.

In an isosceles triangle, the bisector, median and height drawn to the base are the same. The converse is also true: if the bisector, median and height drawn from one vertex are the same, then the triangle is isosceles.

Let's remember another theorem.

Theorem: the sum of the angles of a triangle is 180 degrees

Findings:

- if we know any two angles in a triangle, then we can always find the third angle.

In a right triangle, the sum of the acute angles is 90 degrees.

The following property should be mentioned separately. Only with its help it will be possible to quickly solve problems where we are talking about the median in a right triangle. First the fact itself:

Median in a right triangle drawn from

the right angle to the hypotenuse is half of it

RH = 0.5AC AO = OS = RH

That is, triangles AOB and BOC are isosceles, and the angles at their bases are equal. These conclusions (about angles) are extremely necessary for solving a number of problems.

A little explanation. Why is the median in this case equal to half the hypotenuse? Here it is worth recalling the information that any triangle built on the diameter of a circle, the vertex of which belongs to this circle, is rectangular, this was discussed in detail.

Look: AO, OS and OB are radii, they are equal to a circle. And, of course, OB will be equal to half AC. Therefore, the median in any right triangle drawn to the hypotenuse will be equal to half of it.

Sincerely, Alexander

P.S: I would be grateful if you tell about the site in social networks.