4 wonderful points of a triangle and their properties. Four wonderful points of the triangle

There are so-called four remarkable points in a triangle: the point of intersection of the medians. The point of intersection of the bisectors, the point of intersection of the heights and the point of intersection of the perpendicular bisectors. Let's consider each of them.

Point of intersection of the medians of a triangle

Theorem 1

On the intersection of the medians of a triangle: The medians of a triangle intersect at one point and divide the intersection point in a ratio of $2:1$ starting from the vertex.

Proof.

Consider triangle $ABC$, where $(AA)_1,\ (BB)_1,\ (CC)_1$ is its median. Since the medians divide the sides in half. Consider the middle line $A_1B_1$ (Fig. 1).

Figure 1. Medians of a triangle

By Theorem 1, $AB||A_1B_1$ and $AB=2A_1B_1$, hence $\angle ABB_1=\angle BB_1A_1,\ \angle BAA_1=\angle AA_1B_1$. Hence the triangles $ABM$ and $A_1B_1M$ are similar according to the first triangle similarity criterion. Then

Similarly, it is proved that

The theorem has been proven.

Intersection point of the bisectors of a triangle

Theorem 2

On the intersection of the bisectors of a triangle: The bisectors of a triangle intersect at one point.

Proof.

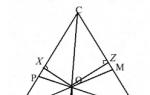
Consider triangle $ABC$, where $AM,\ BP,\ CK$ are its bisectors. Let the point $O$ be the intersection point of the bisectors $AM\ and\ BP$. Draw from this point perpendicular to the sides of the triangle (Fig. 2).

Figure 2. Bisectors of a triangle

Theorem 3

Each point of the bisector of a non-expanded angle is equidistant from its sides.

By Theorem 3, we have: $OX=OZ,\ OX=OY$. Hence $OY=OZ$. Hence the point $O$ is equidistant from the sides of the angle $ACB$ and therefore lies on its bisector $CK$.

The theorem has been proven.

Intersection point of the perpendicular bisectors of a triangle

Theorem 4

The perpendicular bisectors of the sides of a triangle intersect at one point.

Proof.

Let a triangle $ABC$ be given, $n,\ m,\ p$ its perpendicular bisectors. Let the point $O$ be the intersection point of the perpendicular bisectors $n\ and\ m$ (Fig. 3).

Figure 3. Perpendicular bisectors of a triangle

For the proof we need the following theorem.

Theorem 5

Each point of the perpendicular bisector to a segment is equidistant from the ends of the given segment.

By Theorem 3, we have: $OB=OC,\ OB=OA$. Hence $OA=OC$. This means that the point $O$ is equidistant from the ends of the segment $AC$ and, therefore, lies on its perpendicular bisector $p$.

The theorem has been proven.

The point of intersection of the altitudes of the triangle

Theorem 6

The heights of a triangle or their extensions intersect at one point.

Proof.

Consider triangle $ABC$, where $(AA)_1,\ (BB)_1,\ (CC)_1$ is its height. Draw a line through each vertex of the triangle parallel to the side opposite the vertex. We get a new triangle $A_2B_2C_2$ (Fig. 4).

Figure 4. Heights of a triangle

Since $AC_2BC$ and $B_2ABC$ are parallelograms with a common side, then $AC_2=AB_2$, that is, point $A$ is the midpoint of side $C_2B_2$. Similarly, we get that the point $B$ is the midpoint of the side $C_2A_2$, and the point $C$ is the midpoint of the side $A_2B_2$. From the construction we have that $(CC)_1\bot A_2B_2,\ (BB)_1\bot A_2C_2,\ (AA)_1\bot C_2B_2$. Hence $(AA)_1,\ (BB)_1,\ (CC)_1$ are the perpendicular bisectors of triangle $A_2B_2C_2$. Then, by Theorem 4, we have that the heights $(AA)_1,\ (BB)_1,\ (CC)_1$ intersect at one point.

In this lesson, we will look at four wonderful points of the triangle. We will dwell on two of them in detail, recall the proofs of important theorems and solve the problem. The remaining two we recall and characterize.

Subject:Repetition of the 8th grade geometry course

Lesson: Four Remarkable Points of a Triangle

A triangle is, first of all, three segments and three angles, so the properties of segments and angles are fundamental.

Segment AB is given. Any segment has a middle, and a perpendicular can be drawn through it - we denote it by p. Thus p is the perpendicular bisector.

Theorem (basic property of the perpendicular bisector)

Any point lying on the perpendicular bisector is equidistant from the ends of the segment.

Prove that

Proof:

Consider triangles and (see Fig. 1). They are rectangular and equal, because. have a common leg OM, and the legs of AO and OB are equal by condition, thus, we have two right-angled triangles equal in two legs. It follows that the hypotenuses of the triangles are also equal, that is, which was to be proved.

Rice. one

The converse theorem is true.

Theorem

Each point equidistant from the ends of a segment lies on the perpendicular bisector to this segment.

The segment AB is given, the median perpendicular to it p, the point M, equidistant from the ends of the segment (see Fig. 2).

Prove that the point M lies on the perpendicular bisector to the segment.

Rice. 2

Proof:

Let's consider a triangle. It is isosceles, as by condition. Consider the median of the triangle: point O is the midpoint of the base AB, OM is the median. According to the property of an isosceles triangle, the median drawn to its base is both a height and a bisector. Hence it follows that . But the line p is also perpendicular to AB. We know that a single perpendicular to the segment AB can be drawn to the point O, which means that the lines OM and p coincide, hence it follows that the point M belongs to the line p, which was required to be proved.

If it is necessary to describe a circle about one segment, this can be done, and there are infinitely many such circles, but the center of each of them will lie on the perpendicular bisector to the segment.

The perpendicular bisector is said to be the locus of points equidistant from the ends of a segment.

The triangle consists of three segments. Let's draw mid-perpendiculars to two of them and get the point O of their intersection (see Fig. 3).

Point O belongs to the perpendicular bisector to the side BC of the triangle, which means that it is equidistant from its vertices B and C, let's denote this distance as R:.

In addition, the point O is located on the perpendicular bisector to the segment AB, i.e. , however , from here .

Thus, the point O of the intersection of two midpoints

Rice. 3

perpendiculars of the triangle is equidistant from its vertices, which means that it also lies on the third perpendicular bisector.

We have repeated the proof of an important theorem.

The three perpendicular bisectors of a triangle intersect at one point - the center of the circumscribed circle.

So, we have considered the first remarkable point of a triangle - the point of intersection of its perpendicular bisectors.

Let's move on to the property of an arbitrary angle (see Fig. 4).

Given an angle , its bisector AL, point M lies on the bisector.

Rice. 4

If the point M lies on the bisector of the angle, then it is equidistant from the sides of the angle, that is, the distances from the point M to AC and to the BC of the sides of the angle are equal.

Proof:

Consider triangles and . These are right-angled triangles, and they are equal, because. have a common hypotenuse AM, and the angles and are equal, since AL is the bisector of angle . Thus, right-angled triangles are equal in hypotenuse and acute angle, hence it follows that , which was required to be proved. Thus, a point on the bisector of an angle is equidistant from the sides of that angle.

The converse theorem is true.

Theorem

If a point is equidistant from the sides of a non-expanded angle, then it lies on its bisector (see Fig. 5).

An undeveloped angle is given, point M, such that the distance from it to the sides of the angle is the same.

Prove that the point M lies on the bisector of the angle.

Rice. 5

Proof:

The distance from a point to a line is the length of the perpendicular. Draw from the point M perpendiculars MK to side AB and MP to side AC.

Consider triangles and . These are right-angled triangles, and they are equal, because. have a common hypotenuse AM, legs MK and MR are equal by condition. Thus, right triangles are equal in hypotenuse and leg. From the equality of triangles follows the equality of the corresponding elements, equal angles lie against equal legs, thus, , therefore, the point M lies on the bisector of the given angle.

If it is necessary to inscribe a circle in an angle, this can be done, and there are infinitely many such circles, but their centers lie on the bisector of the given angle.

The bisector is said to be the locus of points equidistant from the sides of an angle.

A triangle is made up of three corners. We construct the bisectors of two of them, we get the point O of their intersection (see Fig. 6).

Point O lies on the bisector of the angle, which means that it is equidistant from its sides AB and BC, let's denote the distance as r:. Also, the point O lies on the bisector of the angle , which means that it is equidistant from its sides AC and BC: , , hence .

It is easy to see that the point of intersection of the bisectors is equidistant from the sides of the third angle, which means that it lies on

Rice. 6

angle bisector. Thus, all three bisectors of a triangle intersect at one point.

So, we remembered the proof of another important theorem.

The bisectors of the angles of a triangle intersect at one point - the center of the inscribed circle.

So, we have considered the second wonderful point of the triangle - the intersection point of the bisectors.

We examined the bisector of an angle and noted its important properties: the points of the bisector are equidistant from the sides of the angle, in addition, the segments of tangents drawn to the circle from one point are equal.

Let's introduce some notation (see Fig. 7).

Denote equal segments of tangents by x, y and z. The side BC lying opposite the vertex A is denoted as a, similarly AC as b, AB as c.

Rice. 7

Problem 1: In a triangle, the semiperimeter and side length a are known. Find the length of the tangent drawn from the vertex A - AK, denoted by x.

Obviously, the triangle is not completely defined, and there are many such triangles, but it turns out that they have some elements in common.

For problems in which we are talking about an inscribed circle, we can propose the following solution technique:

1. Draw bisectors and get the center of the inscribed circle.

2. From the center O, draw perpendiculars to the sides and get points of contact.

3. Mark equal tangents.

4. Write out the connection between the sides of the triangle and the tangents.

Point of intersection of the medians of a triangle

Theorem 1

On the intersection of the medians of a triangle: The medians of a triangle intersect at one point and divide the intersection point in a ratio of $2:1$ starting from the vertex.

Proof.

Consider triangle $ABC$, where $(AA)_1,\ (BB)_1,\ (CC)_1$ is its median. Since the medians divide the sides in half. Consider the middle line $A_1B_1$ (Fig. 1).

Figure 1. Medians of a triangle

Similarly, it is proved that

The theorem has been proven.

Intersection point of the bisectors of a triangle

Theorem 2

On the intersection of the bisectors of a triangle: The bisectors of a triangle intersect at one point.

Proof.

Figure 2. Bisectors of a triangle

Theorem 3

Each point of the bisector of a non-expanded angle is equidistant from its sides.

By Theorem 3, we have: $OX=OZ,\ OX=OY$. Hence $OY=OZ$. Hence the point $O$ is equidistant from the sides of the angle $ACB$ and therefore lies on its bisector $CK$.

The theorem has been proven.

Intersection point of the perpendicular bisectors of a triangle

Theorem 4

The perpendicular bisectors of the sides of a triangle intersect at one point.

Proof.

Let a triangle $ABC$ be given, $n,\ m,\ p$ its perpendicular bisectors. Let the point $O$ be the intersection point of the perpendicular bisectors $n\ and\ m$ (Fig. 3).

Figure 3. Perpendicular bisectors of a triangle

For the proof we need the following theorem.

Theorem 5

Each point of the perpendicular bisector to a segment is equidistant from the ends of the given segment.

By Theorem 3, we have: $OB=OC,\ OB=OA$. Hence $OA=OC$. This means that the point $O$ is equidistant from the ends of the segment $AC$ and, therefore, lies on its perpendicular bisector $p$.

The theorem has been proven.

The point of intersection of the altitudes of the triangle

Theorem 6

The heights of a triangle or their extensions intersect at one point.

Proof.

Figure 4. Heights of a triangle

Subject:Repetition of the 8th grade geometry course

Lesson: Four Remarkable Points of a Triangle

A triangle is, first of all, three segments and three angles, so the properties of segments and angles are fundamental.

Segment AB is given. Any segment has a middle, and a perpendicular can be drawn through it - we denote it by p. Thus p is the perpendicular bisector.

Theorem (basic property of the perpendicular bisector)

Any point lying on the perpendicular bisector is equidistant from the ends of the segment.

Prove that

Proof:

Rice. one

The converse theorem is true.

Theorem

Each point equidistant from the ends of a segment lies on the perpendicular bisector to this segment.

The segment AB is given, the median perpendicular to it p, the point M, equidistant from the ends of the segment (see Fig. 2).

Prove that the point M lies on the perpendicular bisector to the segment.

Rice. 2

Proof:

The perpendicular bisector is said to be the locus of points equidistant from the ends of a segment.

The triangle consists of three segments. Let's draw mid-perpendiculars to two of them and get the point O of their intersection (see Fig. 3).

Point O belongs to the perpendicular bisector to the side BC of the triangle, which means that it is equidistant from its vertices B and C, let's denote this distance as R:.

In addition, the point O is located on the perpendicular bisector to the segment AB, i.e. , however , from here .

Thus, the point O of the intersection of two midpoints

Rice. 3

perpendiculars of the triangle is equidistant from its vertices, which means that it also lies on the third perpendicular bisector.

We have repeated the proof of an important theorem.

The three perpendicular bisectors of a triangle intersect at one point - the center of the circumscribed circle.

So, we have considered the first remarkable point of a triangle - the point of intersection of its perpendicular bisectors.

Let's move on to the property of an arbitrary angle (see Fig. 4).

Given an angle , its bisector AL, point M lies on the bisector.

Rice. 4

If the point M lies on the bisector of the angle, then it is equidistant from the sides of the angle, that is, the distances from the point M to AC and to the BC of the sides of the angle are equal.

Proof:

The converse theorem is true.

Theorem

If a point is equidistant from the sides of a non-expanded angle, then it lies on its bisector (see Fig. 5).

An undeveloped angle is given, point M, such that the distance from it to the sides of the angle is the same.

Prove that the point M lies on the bisector of the angle.

Rice. 5

Proof:

The distance from a point to a line is the length of the perpendicular. Draw from the point M perpendiculars MK to side AB and MP to side AC.

If it is necessary to inscribe a circle in an angle, this can be done, and there are infinitely many such circles, but their centers lie on the bisector of the given angle.

The bisector is said to be the locus of points equidistant from the sides of an angle.

A triangle is made up of three corners. We construct the bisectors of two of them, we get the point O of their intersection (see Fig. 6).

It is easy to see that the point of intersection of the bisectors is equidistant from the sides of the third angle, which means that it lies on

Rice. 6

angle bisector. Thus, all three bisectors of a triangle intersect at one point.

So, we remembered the proof of another important theorem.

The bisectors of the angles of a triangle intersect at one point - the center of the inscribed circle.

So, we have considered the second wonderful point of the triangle - the intersection point of the bisectors.

Let's introduce some notation (see Fig. 7).

Denote equal segments of tangents by x, y and z. The side BC lying opposite the vertex A is denoted as a, similarly AC as b, AB as c.

Rice. 7

Problem 1: In a triangle, the semiperimeter and side length a are known. Find the length of the tangent drawn from the vertex A - AK, denoted by x.

Obviously, the triangle is not completely defined, and there are many such triangles, but it turns out that they have some elements in common.

For problems in which we are talking about an inscribed circle, we can propose the following solution technique:

1. Draw bisectors and get the center of the inscribed circle.

2. From the center O, draw perpendiculars to the sides and get points of contact.

3. Mark equal tangents.

4. Write out the connection between the sides of the triangle and the tangents.

Introduction

The objects of the world around us have certain properties, which are studied by various sciences.

Geometry is a branch of mathematics that considers various shapes and their properties, its roots go back to the distant past.

In the fourth book of the "Beginnings", Euclid solves the problem: "Inscribe a circle in a given triangle." It follows from the solution that the three bisectors of the interior angles of a triangle intersect at one point - the center of the inscribed circle. From the solution of another problem of Euclid, it follows that the perpendiculars restored to the sides of the triangle at their midpoints also intersect at one point - the center of the circumscribed circle. The "Principles" does not say that the three heights of a triangle intersect at one point, called the orthocenter (the Greek word "orthos" means "straight", "correct"). This proposal was, however, known to Archimedes. The fourth singular point of the triangle is the point of intersection of the medians. Archimedes proved that it is the center of gravity (barycenter) of the triangle.

The above four points were given special attention, and since the 18th century they have been called "remarkable" or "special" points of the triangle. The study of the properties of a triangle associated with these and other points served as the beginning for the creation of a new branch of elementary mathematics - "the geometry of a triangle" or "a new geometry of a triangle", one of the founders of which was Leonhard Euler.

In 1765, Euler proved that in any triangle the orthocenter, barycenter and center of the circumscribed circle lie on the same straight line, later called "Euler's line". In the twenties of the 19th century, the French mathematicians J. Poncelet, Ch. Brianchon and others independently established the following theorem: the bases of the medians, the bases of the heights and the midpoints of the segments of the heights connecting the orthocenter with the vertices of the triangle lie on the same circle. This circle is called the "circle of nine points", or the "circle of Feuerbach", or the "circle of Euler". K. Feuerbach established that the center of this circle lies on the Euler line.

“I think that we have never lived in such a geometrical period until now. Everything around is geometry. These words, spoken by the great French architect Le Corbusier at the beginning of the 20th century, very accurately characterize our time. The world in which we live is filled with the geometry of houses and streets, mountains and fields, the creations of nature and man.

We were interested in the so-called "wonderful points of the triangle."

After reading the literature on this topic, we fixed for ourselves the definitions and properties of the remarkable points of the triangle. But our work did not end there, and we wanted to explore these points ourselves.

So goal given work - the study of some wonderful points and lines of the triangle, the application of the knowledge gained to solving problems. In the process of achieving this goal, the following stages can be distinguished:

Selection and study of educational material from various sources of information, literature;

The study of the basic properties of the remarkable points and lines of the triangle;

Generalization of these properties and proof of necessary theorems;

Solving problems related to the remarkable points of the triangle.

ChapterI. Wonderful triangle dots and lines

1.1 Point of intersection of the midperpendiculars to the sides of a triangle

The perpendicular bisector is a straight line passing through the midpoint of a segment, perpendicular to it. We already know the theorem characterizing the property of the perpendicular bisector: each point of the perpendicular bisector to the segment is equidistant from its ends and vice versa, if the point is equidistant from the ends of the segment, then it lies on the perpendicular bisector.

The polygon is called inscribed into a circle if all its vertices belong to the circle. The circle is called circumscribed near the polygon.

A circle can be circumscribed around any triangle. Its center is the point of intersection of the medial perpendiculars to the sides of the triangle.

Let the point O be the point of intersection of the perpendicular bisectors to the sides of the triangle AB and BC.

Conclusion: Thus, if the point O is the point of intersection of the midperpendiculars to the sides of the triangle, then OA = OS = OB, i.e. point O is equidistant from all vertices of the triangle ABC, which means that it is the center of the circumscribed circle.


acute-angled	obtuse	rectangular

Consequences

sin γ \u003d c / 2R \u003d c / sin γ \u003d 2R.

It is proved similarly a/ sin α =2R, b/sin β =2R.

Thus:

This property is called the sine theorem.

In mathematics, it often happens that objects defined in very different ways turn out to be the same.

Example. Let A1, B1, C1 be the midpoints of the sides ∆ABS BC, AC, AB, respectively. Show that the circles circumscribed about the triangles AB1C1, A1B1C, A1BC1 intersect at one point. Moreover, this point is the center of the circumscribed about ∆ABS circle.

Consider the segment AO and construct a circle on this segment, as on a diameter. Points C1 and B1 fall on this circle, because are vertices of right angles based on AO. Points A, C1, B1 lie on a circle = this circle is circumscribed about ∆AB1C1.

Similarly, we will draw a segment BO and construct a circle on this segment, as on a diameter. This will be a circle circumscribed about ∆BC1 A1.

Let's draw a segment CO and build a circle on this segment, as on a diameter. This will be the circumscribed circle

These three circles pass through the point O - the center of the circle circumscribed about ∆ABC.

Generalization. If arbitrary points A 1 , B 1 , C 1 are taken on the sides ∆ABC AC, BC, AC, then the circles circumscribed about the triangles AB 1 C 1 , A 1 B 1 C, A 1 BC 1 intersect at one point.

1.2 Point of intersection of the bisectors of a triangle

The converse statement is also true: if a point is equidistant from the sides of an angle, then it lies on its bisector.

It is useful to mark the halves of one corner with the same letters:

OAF=OAD= α, OBD=OBE= β, OCE=OCF= γ.

Let the point O be the intersection point of the bisectors of angles A and B. By the property of a point lying on the bisector of angle A, OF=OD=r. By the property of a point lying on the bisector of angle B, OE=OD=r. Thus, OE=OD= OF=r= point O is equidistant from all sides of the triangle ABC, i.e. O is the center of the inscribed circle. (Point O is the only one).

Conclusion: Thus, if the point O is the point of intersection of the bisectors of the angles of the triangle, then OE=OD= OF=r, i.e. point O is equidistant from all sides of the triangle ABC, which means that it is the center of the inscribed circle. The point O - the intersection of the bisectors of the angles of the triangle is a wonderful point of the triangle.

Consequences:

From the equality of triangles AOF and AOD (Figure 1) along the hypotenuse and acute angle, it follows that AF = AD . From the equality of triangles OBD and OBE it follows that BD = BE , It follows from the equality of triangles COE and COF that With F = CE . Thus, the segments of tangents drawn to the circle from one point are equal.

AF=AD= z, BD=BE= y, СF=CE= x

a=x+y (1), b= x+z (2), c= x+y (3).

+ (2) – (3), then we get: a+b-c=x+ y+ x+ z- z- y = a+b-c= 2x =

x=( b + c - a)/2

Similarly: (1) + (3) - (2), we get: y = (a + c -b)/2.

Similarly: (2) + (3) - (1), we get: z= (a +b - c)/2.

The angle bisector of a triangle divides the opposite side into segments proportional to the adjacent sides.

1.3 Point of intersection of the medians of a triangle (centroid)

Proof 1. Let A 1 , B 1 and C 1 be the midpoints of sides BC, CA and AB of triangle ABC, respectively (Fig. 4).

Let G be the intersection point of two medians AA 1 and BB 1 . Let us first prove that AG:GA 1 = BG:GB 1 = 2.

To do this, take the midpoints P and Q of segments AG and BG. According to the triangle midline theorem, the segments B 1 A 1 and PQ are equal to half of the side AB and are parallel to it. Therefore, the quadrilateral A 1 B 1 is a PQ-parallelogram. Then the intersection point G of its diagonals PA 1 and QB 1 bisects each of them. Therefore, the points P and G divide the median of AA 1 into three equal parts, and the points Q and G divide the median of BB 1 also into three equal parts. So, the point G of the intersection of the two medians of the triangle divides each of them in a ratio of 2:1, counting from the top.

The point of intersection of the medians of a triangle is called centroid or center of gravity triangle. This name is due to the fact that it is at this point that the center of gravity of a homogeneous triangular plate is located.

1.4 Point of intersection of the heights of the triangle (orthocenter)

1.5 Point Torricelli

The path given is triangle ABC. The Torricelli point of this triangle is such a point O, from which the sides of this triangle are visible at an angle of 120°, i.e. angles AOB, AOC and BOC are 120°.

Let us prove that if all the angles of the triangle are less than 120°, then the Torricelli point exists.

On the side AB of the triangle ABC, we construct an equilateral triangle ABC "(Fig. 6, a), and describe a circle around it. The segment AB subtends the arc of this circle with a value of 120 °. Therefore, the points of this arc, other than A and B, have the property that the segment AB is visible from them at an angle of 120 °. Similarly, on the AC side of the triangle ABC, we construct an equilateral triangle ACB "(Fig. 6, a), and describe a circle around it. Points of the corresponding arc, other than A and C, have the property that the segment AC is visible from them at an angle of 120°. In the case when the angles of the triangle are less than 120°, these arcs intersect at some interior point O. In this case, ∟AOB = 120°, ∟AOC = 120°. Therefore, ∟BOC = 120°. Therefore, the point O is the desired one.

In the case when one of the angles of the triangle, for example ABC, is equal to 120°, the point of intersection of the arcs of the circles will be point B (Fig. 6, b). In this case, the Torricelli point does not exist, since it is impossible to talk about the angles at which sides AB and BC are visible from this point.

In the case when one of the angles of the triangle, for example, ABC, is greater than 120° (Fig. 6, c), the corresponding arcs of the circles do not intersect, and the Torricelli point also does not exist.

Related to the Torricelli point is Fermat's problem (which we will consider in Chapter II) of finding the point from which the sum of the distances from which to three given points is the smallest.

1.6 Circle of nine points

Indeed, A 3 B 2 is the midline of triangle AHC and, consequently, A 3 B 2 || CC1. B 2 A 2 is the middle line of triangle ABC and, therefore, B 2 A 2 || AB. Since CC 1 ┴ AB, then A 3 B 2 A 2 = 90°. Similarly, A 3 C 2 A 2 = 90°. Therefore points A 2 , B 2 , C 2 , A 3 lie on the same circle with diameter A 2 A 3 . Since AA 1 ┴BC, the point A 1 also belongs to this circle. Thus, the points A 1 and A 3 lie on the circumcircle of the triangle A2B2C2. Similarly, it is shown that the points B 1 and B 3 , C 1 and C 3 lie on this circle. So all nine points lie on the same circle.

In this case, the center of the circle of nine points lies in the middle between the center of the intersection of the heights and the center of the circumscribed circle. Indeed, let in triangle ABC (Fig. 9), point O be the center of the circumscribed circle; G is the point of intersection of the medians. H point of intersection of heights. It is required to prove that the points O, G, H lie on the same straight line and the center of the circle of nine points N divides the segment OH in half.

Consider a homothety centered at G and with coefficient -0.5. Vertices A, B, C of triangle ABC will go to points A 2 , B 2 , C 2 respectively. The heights of the triangle ABC will go to the heights of the triangle A 2 B 2 C 2 and, consequently, the point H will go to the point O. Therefore, the points O, G, H will lie on one straight line.

Let us show that the midpoint N of the segment OH is the center of the circle of nine points. Indeed, C 1 C 2 is the nine-point chord of the circle. Therefore, the perpendicular bisector to this chord is the diameter and intersects OH at the midpoint of N. Similarly, the perpendicular bisector to the chord B 1 B 2 is the diameter and intersects OH at the same point N. Hence, N is the center of the circle of nine points. Q.E.D.

Indeed, let P be an arbitrary point lying on the circumcircle of triangle ABC; D, E, F are the bases of the perpendiculars dropped from the point P to the sides of the triangle (Fig. 10). Let us show that the points D, E, F lie on the same straight line.

Note that if AP passes through the center of the circle, then points D and E coincide with vertices B and C. Otherwise, one of the angles ABP or ACP is acute and the other is obtuse. It follows from this that the points D and E will be located on different sides of the line BC, and in order to prove that the points D, E and F lie on the same line, it is enough to check that ∟CEF =∟BED.

Let us describe a circle with diameter CP. Since ∟CFP = ∟CEP = 90°, the points E and F lie on this circle. Therefore, ∟CEF =∟CPF as inscribed angles based on one circular arc. Further, ∟CPF = 90°- ∟PCF = 90°- ∟DBP = ∟BPD. Let's describe a circle with diameter BP. Since ∟BEP = ∟BDP = 90°, the points F and D lie on this circle. Therefore, ∟BPD = ∟BED. Therefore, we finally obtain that ∟CEF =∟BED. So the points D, E, F lie on the same straight line.

ChapterIIProblem solving

Let's start with problems related to the location of bisectors, medians, and heights of a triangle. Their solution, on the one hand, allows you to remember the material covered earlier, and on the other hand, develops the necessary geometric representations, prepares you for solving more complex problems.

Task 1. At angles A and B of triangle ABC (∟A

Decision. Let CD be the height, CE the bisector, then

∟BCD = 90° - ∟B, ∟BCE = (180° - ∟A - ∟B):2.

Therefore, ∟DCE =.

Decision. Let O be the intersection point of the bisectors of triangle ABC (Fig. 1). Let's take advantage of the fact that a larger angle lies opposite the larger side of the triangle. If AB BC, then ∟A

Decision. Let O be the intersection point of the altitudes of triangle ABC (Fig. 2). If AC ∟B. A circle with diameter BC will pass through points F and G. Considering that the smaller of the two chords is the one on which the smaller inscribed angle rests, we get that CG

Proof. On sides AC and BC of triangle ABC, as on diameters, we construct circles. Points A 1 , B 1 , C 1 belong to these circles. Therefore, ∟B 1 C 1 C = ∟B 1 BC, as angles based on the same circular arc. ∟B 1 BC = ∟CAA 1 as angles with mutually perpendicular sides. ∟CAA 1 = ∟CC 1 A 1 as angles based on the same circular arc. Therefore, ∟B 1 C 1 C = ∟CC 1 A 1 , i.e. CC 1 is the bisector of angle B 1 C 1 A 1 . Similarly, it is shown that AA 1 and BB 1 are bisectors of angles B 1 A 1 C 1 and A 1 B 1 C 1 .

The considered triangle, whose vertices are the bases of the altitudes of a given acute-angled triangle, gives an answer to one of the classical extremal problems.

Decision. Let ABC be a given acute triangle. On its sides it is required to find such points A 1 , B 1 , C 1 for which the perimeter of the triangle A 1 B 1 C 1 would be the smallest (Fig. 4).

Let us first fix the point C 1 and look for the points A 1 and B 1 for which the perimeter of the triangle A 1 B 1 C 1 is the smallest (for the given position of the point C 1).

To do this, consider the points D and E symmetrical to the point C 1 with respect to the lines AC and BC. Then B 1 C 1 \u003d B 1 D, A 1 C 1 \u003d A 1 E and, therefore, the perimeter of the triangle A 1 B 1 C 1 will be equal to the length of the polyline DB 1 A 1 E. It is clear that the length of this polyline is the smallest if the points B 1 , A 1 lie on the line DE.

We will now change the position of the point C 1 and look for such a position at which the perimeter of the corresponding triangle A 1 B 1 C 1 is the smallest.

Since point D is symmetrical to C 1 with respect to AC, then CD = CC 1 and ACD=ACC 1 . Similarly, CE=CC 1 and BCE=BCC 1 . Therefore, triangle CDE is isosceles. Its side is equal to CC 1 . The base DE is equal to the perimeter P triangle A 1 B 1 C 1 . The angle DCE is equal to twice the angle ACB of the triangle ABC and, therefore, does not depend on the position of the point C 1 .

In an isosceles triangle with a given angle at the apex, the smaller the base, the smaller the side. Therefore, the smallest value of the perimeter P is achieved in the case of the smallest value of CC 1 . This value is taken if CC 1 is the height of triangle ABC. Thus, the required point C 1 on the side AB is the base of the height drawn from the top C.

Note that we could first fix not the point C 1 , but the point A 1 or the point B 1 and we would get that A 1 and B 1 are the bases of the corresponding altitudes of the triangle ABC.

From this it follows that the desired triangle, the smallest perimeter, inscribed in a given acute-angled triangle ABC is a triangle whose vertices are the bases of the altitudes of triangle ABC.

Decision. Let us prove that if the angles of the triangle are less than 120°, then the desired point in the Steiner problem is the Torricelli point.

Let's rotate the triangle ABC around the vertex C by an angle of 60°, fig. 7. Get the triangle A'B'C. Take an arbitrary point O in triangle ABC. When turning, it will go to some point O’. Triangle OO'C is equilateral since CO = CO' and ∟OCO' = 60°, hence OC = OO'. Therefore, the sum of the lengths of OA + OB + OC will be equal to the length of the polyline AO + OO’ + O’B’. It is clear that the length of this polyline takes on the smallest value if the points A, O, O', B' lie on the same straight line. If O is a Torricelli point, then it is. Indeed, ∟AOC = 120°, ∟COO" = 60°. Therefore, the points A, O, O' lie on the same line. Similarly, ∟CO'O = 60°, ∟CO"B" = 120°. Therefore, the points O, O', B' lie on the same line, which means that all the points A, O, O', B' lie on the same line.

Conclusion

The geometry of a triangle, along with other sections of elementary mathematics, makes it possible to feel the beauty of mathematics in general and can become for someone the beginning of the path to "big science".

Geometry is an amazing science. Her history spans more than one millennium, but each meeting with her is able to endow and enrich (both the student and the teacher) with the exciting novelty of a small discovery, the amazing joy of creativity. Indeed, any problem of elementary geometry is, in essence, a theorem, and its solution is a modest (and sometimes huge) mathematical victory.

Historically, geometry began with a triangle, so for two and a half millennia the triangle has been a symbol of geometry. School geometry can only then become interesting and meaningful, only then can it become proper geometry, when a deep and comprehensive study of the triangle appears in it. Surprisingly, the triangle, despite its apparent simplicity, is an inexhaustible object of study - no one, even in our time, dares to say that he has studied and knows all the properties of a triangle.

In this paper, the properties of bisectors, medians, perpendicular bisectors and altitudes of a triangle were considered, the number of remarkable points and lines of a triangle was expanded, theorems were formulated and proved. A number of problems on the application of these theorems have been solved.

The presented material can be used both in basic lessons and in optional classes, as well as in preparation for centralized testing and mathematics olympiads.

Bibliography

Berger M. Geometry in two volumes - M: Mir, 1984.

Kiselev A.P. Elementary geometry. – M.: Enlightenment, 1980.

Kokseter G.S., Greitzer S.L. New encounters with geometry. – M.: Nauka, 1978.

Latotin L.A., Chebotaravskiy B.D. Mathematics 9. - Minsk: Narodnaya Asveta, 2014.

Prasolov V.V. Problems in planimetry. - M.: Nauka, 1986. - Part 1.

Scanavi M. I. Mathematics. Problems with solutions. - Rostov-on-Don: Phoenix, 1998.

Sharygin I.F. Problems in geometry: Planimetry. – M.: Nauka, 1986.