Hanapin ang mga katangiang numero ng isang matrix online. Eigenvalues (mga numero) at eigenvectors. Mga halimbawa ng mga solusyon

Kahulugan 9.3. Vector X tinawag sariling vector matrice PERO kung may ganyang numero λ, na taglay ng pagkakapantay-pantay: PERO X= λ X, iyon ay, ang resulta ng pag-aaplay sa X linear transformation na ibinigay ng matrix PERO, ay ang multiplikasyon ng vector na ito sa numero λ . Ang numero mismo λ tinawag sariling numero matrice PERO.

Pagpapalit sa mga formula (9.3) x` j = λx j , nakakakuha kami ng isang sistema ng mga equation para sa pagtukoy ng mga coordinate ng eigenvector:

. (9.5)

Ang linear homogenous na sistemang ito ay magkakaroon lamang ng di-trivial na solusyon kung ang pangunahing determinant nito ay 0 (Cramer's rule). Sa pamamagitan ng pagsulat ng kundisyong ito sa anyo:

nakakakuha tayo ng equation para sa pagtukoy ng eigenvalues λ tinawag katangian equation. Sa madaling sabi, maaari itong ilarawan bilang mga sumusunod:

| A-λE | = 0, (9.6)

dahil ang kaliwang bahagi nito ay ang determinant ng matrix A-λE. Polinomyal na may kinalaman sa λ | A-λE| tinawag katangiang polinomyal matrices a.

Mga katangian ng katangiang polynomial:

1) Ang katangiang polynomial ng isang linear na pagbabago ay hindi nakasalalay sa pagpili ng batayan. Patunay. (tingnan ang (9.4)), ngunit kaya naman, . Kaya, hindi nakasalalay sa pagpili ng batayan. Samakatuwid, at | A-λE| hindi nagbabago sa paglipat sa isang bagong batayan.

2) Kung ang matris PERO ang linear transformation ay simetriko(mga. a ij = isang ji), kung gayon ang lahat ng mga ugat ng katangian na equation (9.6) ay mga tunay na numero.

Mga katangian ng eigenvalues at eigenvectors:

1) Kung pipili tayo ng batayan mula sa eigenvectors x 1, x 2, x 3 naaayon sa eigenvalues λ 1 , λ 2 , λ 3 matrice PERO, pagkatapos sa batayan na ito ang linear transformation A ay may dayagonal na matrix:

(9.7) Ang patunay ng property na ito ay sumusunod sa kahulugan ng eigenvectors.

2) Kung ang pagbabagong-anyo eigenvalues PERO ay magkaiba, pagkatapos ay ang katumbas eigenvectors ay linearly independent.

3) Kung ang katangian polynomial ng matrix PERO ay may tatlong magkakaibang ugat, pagkatapos ay sa ilang batayan ang matris PERO ay may dayagonal na hugis.

Hanapin natin ang eigenvalues at eigenvectors ng matrix Gawin natin ang katangiang equation: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Hanapin ang mga coordinate ng eigenvectors na tumutugma sa bawat nahanap na halaga λ. Mula sa (9.5) sumusunod na kung X (1) ={x 1 , x 2 , x 3) ay ang eigenvector na katumbas ng λ 1 = -2, pagkatapos

ay isang collaborative ngunit hindi tiyak na sistema. Ang solusyon nito ay maaaring isulat bilang X (1) ={a,0,-a), kung saan ang a ay anumang numero. Sa partikular, kung kailangan mo iyon | x (1) |=1, X (1) =

Pagpapalit sa system (9.5) λ 2 =3, nakakakuha kami ng isang sistema para sa pagtukoy ng mga coordinate ng pangalawang eigenvector - x (2) ={y1,y2,y3}:

, saan X (2) ={b,-b,b) o, ibinigay | x (2) |=1, x (2) =

Para sa λ 3 = 6 hanapin ang eigenvector x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) o sa normalized na bersyon

x (3) = Ito ay makikita na X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = bc- 2bc + bc= 0. Kaya, ang eigenvectors ng matrix na ito ay pairwise orthogonal.

Lektura 10

Mga parisukat na anyo at ang kanilang koneksyon sa mga simetriko na matrice. Mga katangian ng eigenvectors at eigenvalues ng isang simetriko matrix. Pagbawas ng isang parisukat na anyo sa isang kanonikal na anyo.

Kahulugan 10.1.parisukat na anyo tunay na mga variable x 1, x 2,…, x n ay isang polynomial ng pangalawang degree na may kinalaman sa mga variable na ito na hindi naglalaman ng libreng termino at mga termino ng unang degree.

Mga halimbawa ng mga parisukat na anyo:

(n = 2),

(n = 3). (10.1)

Alalahanin ang kahulugan ng isang simetriko matrix na ibinigay sa huling lecture:

Kahulugan 10.2. Ang square matrix ay tinatawag simetriko, kung , iyon ay, kung ang mga elemento ng matrix ay simetriko na may paggalang sa pangunahing dayagonal ay pantay.

Mga katangian ng eigenvalues at eigenvectors ng isang simetriko matrix:

1) Ang lahat ng eigenvalues ng isang simetriko matrix ay totoo.

Patunay (para sa n = 2).

Hayaan ang matrix PERO mukhang: . Gawin natin ang katangiang equation:

(10.2) Hanapin natin ang discriminant:

Samakatuwid, ang equation ay mayroon lamang tunay na mga ugat.

2) Ang eigenvectors ng isang simetriko matrix ay orthogonal.

Patunay (para sa n= 2).

Ang mga coordinate ng eigenvectors at dapat matugunan ang mga equation.

SISTEMA NG HOMOGENEOUS LINEAR EQUATIONS

sistema ng homogenous linear na equation tinatawag na sistema ng anyo

Ito ay malinaw na sa kasong ito , kasi lahat ng elemento ng isa sa mga column sa mga determinant na ito ay katumbas ng zero.

Dahil ang mga hindi alam ay matatagpuan sa pamamagitan ng mga formula , pagkatapos ay sa kaso kapag Δ ≠ 0, ang sistema ay may natatanging zero na solusyon x = y = z= 0. Gayunpaman, sa maraming mga problema ang tanong kung ang isang homogenous na sistema ay may mga solusyon maliban sa zero ay interesado.

Teorama. Upang ang sistema ng linear homogenous equation ay may nonzero na solusyon, ito ay kinakailangan at sapat na Δ ≠ 0.

Kaya, kung ang determinant ay Δ ≠ 0, kung gayon ang sistema ay may natatanging solusyon. Kung Δ ≠ 0, kung gayon ang sistema ng mga linear homogenous na equation ay may walang katapusang bilang ng mga solusyon.

Mga halimbawa.

Eigenvectors at Matrix Eigenvalues

Hayaang magbigay ng square matrix , X ay ilang matrix-column na ang taas ay tumutugma sa pagkakasunud-sunod ng matrix A. .

Sa maraming problema, kailangang isaalang-alang ang equation para sa X

kung saan ang λ ay ilang numero. Ito ay malinaw na para sa anumang λ ang equation na ito ay may zero na solusyon.

Ang bilang na λ kung saan ang equation na ito ay may mga nonzero na solusyon ay tinatawag eigenvalue matrice A, a X para sa gayong λ ay tinatawag sariling vector matrice A.

Hanapin natin ang eigenvector ng matrix A. Sa abot ng E∙X=X, kung gayon ang matrix equation ay maaaring muling isulat bilang o . Sa pinalawak na anyo, ang equation na ito ay maaaring muling isulat bilang isang sistema ng mga linear na equation. Talaga .

At samakatuwid

Kaya, nakakuha kami ng isang sistema ng homogenous linear equation para sa pagtukoy ng mga coordinate x 1, x2, x 3 vector X. Para sa system na magkaroon ng mga non-zero na solusyon, kinakailangan at sapat na ang determinant ng system ay katumbas ng zero, i.e.

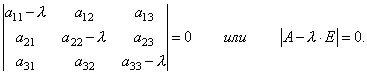
Ito ay isang 3rd degree na equation na may kinalaman sa λ. Ang tawag dito katangian equation matrice A at nagsisilbi upang matukoy ang mga eigenvalues λ.

Ang bawat eigenvalue λ ay tumutugma sa isang eigenvector X, na ang mga coordinate ay tinutukoy mula sa system sa katumbas na halaga ng λ.

Mga halimbawa.

VECTOR ALGEBRA. KONSEPTO NG VECTOR

Kapag nag-aaral ng iba't ibang sangay ng pisika, may mga dami na ganap na natutukoy sa pamamagitan ng pagtatakda ng kanilang mga numerical na halaga, halimbawa, haba, lugar, masa, temperatura, atbp. Ang ganitong mga halaga ay tinatawag na scalar. Gayunpaman, bilang karagdagan sa mga ito, mayroon ding mga dami, para sa pagpapasiya kung saan, bilang karagdagan sa numerical na halaga, kinakailangan ding malaman ang kanilang direksyon sa espasyo, halimbawa, ang puwersa na kumikilos sa katawan, ang bilis at acceleration. ng katawan kapag gumagalaw ito sa kalawakan, ang tensyon magnetic field sa isang partikular na punto sa espasyo, atbp. Ang ganitong mga dami ay tinatawag na mga dami ng vector.

Ipakilala natin ang isang mahigpit na kahulugan.

Direksyon na segment Tawagan natin ang isang segment, na nauugnay sa mga dulo kung saan alam kung alin sa kanila ang una at alin ang pangalawa.

Vector tinatawag ang isang nakadirekta na segment, na may tiyak na haba, i.e. Ito ay isang segment ng isang tiyak na haba, kung saan ang isa sa mga puntong naglilimita dito ay kinuha bilang simula, at ang pangalawa - bilang dulo. Kung ang A ay ang simula ng vector, B ay ang katapusan nito, pagkatapos ay ang vector ay tinutukoy ng simbolo, bilang karagdagan, ang vector ay madalas na tinutukoy ng isang solong titik . Sa figure, ang vector ay ipinahiwatig ng isang segment, at ang direksyon nito sa pamamagitan ng isang arrow.

modyul o mahaba vector ay tinatawag na haba ng nakadirekta na segment na tumutukoy dito. Tinutukoy ng || o ||.

Ang tinatawag na zero vector, na ang simula at pagtatapos ay nag-tutugma, ay tatawagin ding mga vector. Ito ay minarkahan. Ang zero vector ay walang tiyak na direksyon at ang modulus nito ay katumbas ng zero ||=0.

Vectors at tinatawag na collinear kung sila ay matatagpuan sa parehong linya o sa parallel na linya. Sa kasong ito, kung ang mga vector at ay pantay na nakadirekta, isusulat namin ang , kabaligtaran.

Ang mga vector na matatagpuan sa mga tuwid na linya na parallel sa parehong eroplano ay tinatawag coplanar.

Dalawang vector at tinatawag pantay kung sila ay collinear, may parehong direksyon, at pantay ang haba. Sa kasong ito, isulat ang .

Ito ay sumusunod mula sa kahulugan ng pagkakapantay-pantay ng mga vector na ang isang vector ay maaaring ilipat parallel sa sarili nito sa pamamagitan ng paglalagay ng pinagmulan nito sa anumang punto sa espasyo.

Halimbawa.

MGA LINEAR NA OPERASYON SA MGA VECTOR

Pagpaparami ng vector sa isang numero.
Ang produkto ng isang vector sa pamamagitan ng isang numerong λ ay isang bagong vector tulad na:

Ang produkto ng isang vector at isang numerong λ ay tinutukoy ng .

Halimbawa, ay isang vector na tumuturo sa parehong direksyon ng vector at may kalahating haba ng haba ng vector .

Ang ipinasok na operasyon ay may mga sumusunod ari-arian:
Pagdaragdag ng mga vector.
Hayaan at maging dalawang di-makatwirang vectors. Kumuha ng isang arbitrary na punto O at bumuo ng isang vector. Pagkatapos nito, mula sa punto A isantabi ang vector. Ang vector na nagkokonekta sa simula ng unang vector sa dulo ng pangalawa ay tinatawag sum ng mga vector na ito at ipinapahiwatig .

Tinatawag ang formulated definition ng vector addition tuntunin ng paralelogram, dahil ang parehong kabuuan ng mga vector ay maaaring makuha tulad ng sumusunod. Itabi sa punto O mga vector at . Bumuo ng paralelogram sa mga vector na ito OABC. Dahil ang mga vectors , pagkatapos ay ang vector , na siyang dayagonal ng paralelogram na iginuhit mula sa vertex O, ay malinaw naman ang kabuuan ng mga vectors .

Madaling suriin ang mga sumusunod mga katangian ng pagdaragdag ng vector.
Pagkakaiba ng mga vector.
Vector, collinear binigay na vector, katumbas ng haba at magkasalungat na direksyon, ay tinatawag kabaligtaran vector para sa isang vector at tinutukoy ng . Ang kabaligtaran na vector ay maaaring ituring bilang resulta ng pagpaparami ng vector sa pamamagitan ng bilang na λ = –1: .

www.site nagbibigay-daan sa iyo upang mahanap. Ginagawa ng site ang pagkalkula. Sa ilang segundo, maglalabas ang server tamang solusyon. Ang katangian na equation para sa matrix ay isang algebraic expression na makikita ng panuntunan para sa pagkalkula ng determinant matrice matrice, habang sa pangunahing dayagonal magkakaroon ng mga pagkakaiba sa mga halaga ng mga elemento ng dayagonal at ang variable. Kapag nagkalkula katangian equation para sa matrix online, bawat elemento matrice ay pararamihin sa katumbas na iba pang mga elemento matrice. Hanapin sa mode online posible lamang para sa parisukat matrice. Maghanap ng operasyon katangian equation para sa matrix online bumababa sa pagkalkula algebraic sum mga produkto ng mga elemento matrice bilang resulta ng paghahanap ng determinant matrice, para lamang sa layunin ng pagtukoy katangian equation para sa matrix online. Ang operasyong ito ay sumasakop sa isang espesyal na lugar sa teorya matrice, ay nagbibigay-daan sa iyong makahanap ng mga eigenvalues at vectors gamit ang mga ugat . Paghahanap ng gawain katangian equation para sa matrix online ay paramihin ang mga elemento matrice na may kasunod na pagsusuma ng mga produktong ito ayon sa isang tiyak na tuntunin. www.site nahanap katangian equation para sa matrix ibinigay na sukat sa mode online. pagkalkula katangian equation para sa matrix online para sa isang partikular na dimensyon, ito ay paghahanap ng polynomial na may mga numerical o simbolikong coefficient na makikita ng panuntunan para sa pagkalkula ng determinant matrice- bilang kabuuan ng mga produkto ng kaukulang elemento matrice, para lamang sa layunin ng pagtukoy katangian equation para sa matrix online. Paghahanap ng polynomial na may paggalang sa isang variable para sa isang parisukat matrice, bilang kahulugan katangian equation para sa matrix, karaniwan sa teorya matrice. Ang halaga ng mga ugat ng polynomial katangian equation para sa matrix online ginamit upang tukuyin ang mga eigenvector at eigenvalues para sa matrice. Gayunpaman, kung ang determinant matrice magiging zero, kung gayon equation ng katangian ng matrix mananatili pa rin, hindi tulad ng kabaligtaran matrice. Upang makalkula katangian equation para sa matrix o maghanap ng ilan nang sabay-sabay matrices katangian equation, kailangan mong gumastos ng maraming oras at pagsisikap, habang mahahanap ng aming server katangian na equation para sa online na matrix. Sa kasong ito, ang sagot sa pamamagitan ng paghahanap katangian equation para sa matrix online ay magiging tama at may sapat na katumpakan, kahit na ang mga numero kapag hinahanap katangian equation para sa matrix online magiging hindi makatwiran. Online www.site pinapayagan ang mga entry ng character sa mga elemento matrice, ibig sabihin katangian na equation para sa online na matrix ay maaaring katawanin sa isang pangkalahatang simbolikong anyo kapag kinakalkula katangian equation matrix online. Ito ay kapaki-pakinabang upang suriin ang sagot na nakuha kapag nilutas ang problema ng paghahanap katangian equation para sa matrix online gamit ang site www.site. Kapag nagsasagawa ng operasyon ng pagkalkula ng isang polynomial - katangian equation ng matrix, kinakailangang maging matulungin at lubos na nakatuon sa paglutas ng problemang ito. Sa turn, tutulungan ka ng aming site na suriin ang iyong desisyon sa paksa katangian equation matrix online. Kung wala kang oras para sa mahabang pagsusuri ng mga nalutas na problema, kung gayon www.site tiyak na magiging isang maginhawang tool para sa pagsuri kapag naghahanap at nagkalkula katangian equation para sa matrix online.

". Ang unang bahagi ay naglalaman ng mga probisyon na minimal na kinakailangan para sa pag-unawa sa chemometrics, at ang pangalawang bahagi ay naglalaman ng mga katotohanan na kailangan mong malaman para sa mas malalim na pag-unawa sa mga pamamaraan ng multivariate analysis. Ang pagtatanghal ay inilalarawan ng mga halimbawang ginawa sa Excel workbook Matrix.xls na kasama ng dokumentong ito.

Ang mga link sa mga halimbawa ay inilalagay sa teksto bilang mga bagay sa Excel. Ang mga halimbawang ito ay isang abstract na kalikasan; sila ay hindi nakatali sa mga problema ng analytical chemistry. Ang mga tunay na halimbawa ng paggamit ng matrix algebra sa chemometrics ay tinatalakay sa ibang mga teksto na nakatuon sa iba't ibang mga aplikasyon ng chemometric.

Karamihan sa mga sukat na isinagawa sa analytical chemistry ay hindi direkta ngunit hindi direkta. Nangangahulugan ito na sa eksperimento, sa halip na ang halaga ng nais na analyte C (konsentrasyon), isa pang halaga ang nakuha. x(signal) na nauugnay sa ngunit hindi katumbas ng C, i.e. x(C) ≠ C. Bilang isang tuntunin, ang uri ng pagtitiwala x(C) ay hindi kilala, ngunit sa kabutihang palad sa analytical chemistry karamihan sa mga sukat ay proporsyonal. Nangangahulugan ito na bilang ang konsentrasyon ng C in a beses, ang signal X ay tataas ng parehong halaga., i.e. x(a C) = isang x(C). Bilang karagdagan, ang mga signal ay additive din, kaya ang signal mula sa isang sample na naglalaman ng dalawang sangkap na may mga konsentrasyon ng C 1 at C 2 ay magiging ay katumbas ng kabuuan signal mula sa bawat bahagi, i.e. x(C1 + C2) = x(C1)+ x(C2). Ang proporsyonalidad at additivity ay magkasamang nagbibigay linearity. Maraming mga halimbawa ang maaaring ibigay upang ilarawan ang prinsipyo ng linearity, ngunit sapat na upang banggitin ang dalawa sa mga pinaka-kapansin-pansin na mga halimbawa - chromatography at spectroscopy. Ang pangalawang tampok na likas sa eksperimento sa analytical chemistry ay multichannel. Ang mga modernong kagamitan sa pagsusuri ay sabay-sabay na sumusukat ng mga signal para sa maraming mga channel. Halimbawa, ang intensity ng light transmission ay sinusukat para sa ilang mga wavelength nang sabay-sabay, i.e. saklaw. Samakatuwid, sa eksperimento kami ay nakikitungo sa iba't ibang mga signal x 1 , x 2 ,...., x n nagpapakilala sa hanay ng mga konsentrasyon C 1 ,C 2 , ..., C m ng mga sangkap na naroroon sa sistemang pinag-aaralan.

kanin. 1 Spectra

Kaya, ang analytical na eksperimento ay nailalarawan sa pamamagitan ng linearity at multidimensionality. Samakatuwid, maginhawang isaalang-alang ang pang-eksperimentong data bilang mga vector at matrice at manipulahin ang mga ito gamit ang apparatus ng matrix algebra. Ang pagiging mabunga ng diskarteng ito ay inilalarawan ng halimbawang ipinakita sa , na nagpapakita ng tatlong spectra na kinuha para sa 200 wavelength mula 4000 hanggang 4796 cm–1. Una ( x 1) at pangalawa ( x 2) ang spectra ay nakuha para sa mga karaniwang sample kung saan ang mga konsentrasyon ng dalawang sangkap A at B ay kilala: sa unang sample [A] = 0.5, [B] = 0.1, at sa pangalawang sample [A] = 0.2, [ B] = 0.6. Ano ang masasabi tungkol sa isang bago, hindi kilalang sample, ang spectrum ng kung saan ay ipinahiwatig x 3 ?

Isaalang-alang ang tatlong pang-eksperimentong spectra x 1 , x 2 at x 3 bilang tatlong vector ng dimensyon 200. Gamit ang linear algebra, madaling maipakita iyon ng isa x 3 = 0.1 x 1 +0.3 x 2 , kaya ang pangatlong sample ay malinaw na naglalaman lamang ng mga sangkap A at B sa mga konsentrasyon [A] = 0.5×0.1 + 0.2×0.3 = 0.11 at [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Pangunahing impormasyon

1.1 Matrice

Matrix tinatawag na isang hugis-parihaba na talahanayan ng mga numero, halimbawa

kanin. 2 Matris

Ang mga matrice ay tinutukoy ng malalaking titik na naka-bold ( A), at ang kanilang mga elemento - na may kaukulang maliliit na titik na may mga indeks, i.e. a ij . Ang unang index ay binibilang ang mga hilera at ang pangalawang bilang ang mga hanay. Sa chemometrics, kaugalian na italaga ang pinakamataas na halaga ng index na may parehong titik tulad ng index mismo, ngunit sa malalaking titik. Samakatuwid, ang matrix A maaari ding isulat bilang ( a ij , i = 1,..., ako; j = 1,..., J). Para sa halimbawang matrix ako = 4, J= 3 at a 23 = −7.5.

Pares ng mga numero ako at J ay tinatawag na dimensyon ng matrix at tinutukoy bilang ako× J. Ang isang halimbawa ng isang matrix sa chemometrics ay isang set ng spectra na nakuha para sa ako mga sample sa J mga wavelength.

1.2. Ang pinakasimpleng operasyon na may mga matrice

Pwede ang matrices multiply sa mga numero. Sa kasong ito, ang bawat elemento ay pinarami ng numerong ito. Halimbawa -

kanin. 3 Pagpaparami ng matrix sa isang numero

Dalawang matrice ng parehong dimensyon ay maaaring maging element-wise tiklop at ibawas. Halimbawa,

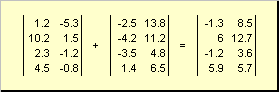
kanin. 4 Pagdaragdag ng matris

Bilang resulta ng multiplikasyon sa isang numero at karagdagan, ang isang matrix ng parehong dimensyon ay nakuha.

Ang zero matrix ay isang matrix na binubuo ng mga zero. Ito ay itinalaga O. Obvious naman yun A+O = A, A−A = O at 0 A = O.

Pwede ang matrix transpose. Sa panahon ng operasyong ito, ang matrix ay binaligtad, i.e. ang mga row at column ay pinagpalit. Ang transposisyon ay ipinahiwatig ng isang gitling, A" o index A t . Kaya, kung A = {a ij , i = 1,..., ako; j = 1,...,J), pagkatapos A t = ( a ji , j = 1,...,J; i = 1,..., ako). Halimbawa

kanin. 5 Transposisyon ng matrix

Obvious naman na ( A t) t = A, (A+B) t = A t+ B t .

1.3. Pagpaparami ng matrix

Pwede ang matrices magparami, ngunit kung mayroon lamang silang naaangkop na mga sukat. Kung bakit ganito ay magiging malinaw mula sa kahulugan. Produkto ng matrix A, sukat ako× K, at mga matrice B, sukat K× J, ay tinatawag na matrix C, sukat ako× J, na ang mga elemento ay mga numero

Kaya para sa produkto AB ito ay kinakailangan na ang bilang ng mga haligi sa kaliwang matrix A ay katumbas ng bilang ng mga hilera sa kanang matrix B. Halimbawa ng produkto ng matrix -

Fig.6 Produkto ng mga matrice

Ang matrix multiplication rule ay maaaring buuin bilang mga sumusunod. Upang mahanap ang isang elemento ng isang matrix C nakatayo sa intersection i-ika linya at j-th column ( c ij) dapat i-multiply ang elemento sa pamamagitan ng elemento i-ika row ng unang matrix A sa j-th column ng pangalawang matrix B at idagdag ang lahat ng mga resulta. Kaya sa halimbawang ipinakita, ang elemento mula sa ikatlong hilera at ang pangalawang hanay ay nakuha bilang kabuuan ng mga produkto na matalino sa elemento ng ikatlong hilera A at ikalawang hanay B

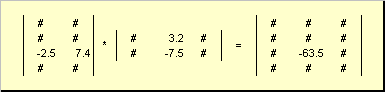
Fig.7 Elemento ng produkto ng matrices

Ang produkto ng mga matrice ay nakasalalay sa pagkakasunud-sunod, i.e. AB ≠ BA, kahit man lang para sa mga dimensional na dahilan. Ito raw ay non-commutative. Gayunpaman, ang produkto ng mga matrice ay nag-uugnay. Ibig sabihin nito ay ABC = (AB)C = A(BC). Bukod dito, ito rin ay distributive, i.e. A(B+C) = AB+AC. Obvious naman yun AO = O.

1.4. Mga parisukat na matrice

Kung ang bilang ng mga haligi ng isang matrix ay katumbas ng bilang ng mga hilera nito ( ako = J=N), kung gayon ang gayong matris ay tinatawag na parisukat. Sa seksyong ito, isasaalang-alang lamang natin ang mga naturang matrice. Sa mga matrice na ito, maaaring isa-isa ng isa ang mga matrice na may mga espesyal na katangian.

Nag-iisa matrix (tinutukoy ako at minsan E) ay isang matrix kung saan ang lahat ng mga elemento ay katumbas ng zero, maliban sa mga dayagonal, na katumbas ng 1, i.e.

Obvious naman AI = IA = A.

Ang matrix ay tinatawag dayagonal, kung ang lahat ng mga elemento nito, maliban sa mga dayagonal ( a ii) ay katumbas ng zero. Halimbawa

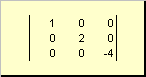
kanin. 8 Diagonal matrix

Matrix A tinawag ang tuktok tatsulok, kung ang lahat ng mga elemento nito na nakahiga sa ibaba ng dayagonal ay katumbas ng zero, i.e. a ij= 0, sa i>j. Halimbawa

kanin. 9 Upper triangular matrix

Ang mas mababang triangular matrix ay tinukoy nang katulad.

Matrix A tinawag simetriko, kung A t = A. Sa ibang salita a ij = a ji. Halimbawa

kanin. 10 Symmetric matrix

Matrix A tinawag orthogonal, kung

A t A = AA t = ako.

Ang matrix ay tinatawag normal kung

1.5. Bakas at determinant

Sumusunod parisukat na matris A(tinutukoy na Tr( A) o Sp( A)) ay ang kabuuan ng mga elementong dayagonal nito,

Halimbawa,

kanin. 11 Matrix na bakas

Obvious naman yun

Sp(α A) = α Sp( A) at

Sp( A+B) = Sp( A)+ Sp( B).

Maaari itong ipakita na

Sp( A) = Sp( A t), Sp( ako) = N,

at ganoon din

Sp( AB) = Sp( BA).

Ang isa pang mahalagang katangian ng isang square matrix ay ito determinant(tinutukoy ng det( A)). Ang kahulugan ng determinant sa pangkalahatang kaso ay medyo kumplikado, kaya magsisimula tayo sa pinakasimpleng opsyon - ang matrix A sukat (2×2). Pagkatapos

Para sa isang (3×3) matrix, ang determinant ay magiging katumbas ng

Sa kaso ng isang matrix ( N× N) ang determinant ay kinakalkula bilang kabuuan 1 2 3 ... N= N! mga termino, na ang bawat isa ay katumbas ng

Mga indeks k 1 , k 2 ,..., k N ay tinukoy bilang lahat ng posibleng ordered permutations r mga numero sa set (1, 2, ... , N). Ang pagkalkula ng determinant ng matrix ay isang kumplikadong pamamaraan, na sa pagsasanay ay isinasagawa gamit ang mga espesyal na programa. Halimbawa,

kanin. 12 Matrix determinant

Napansin lamang namin ang mga halatang katangian:

det( ako) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Mga vector

Kung ang matrix ay may isang hanay lamang ( J= 1), pagkatapos ay tinatawag ang naturang bagay vector. Mas tiyak, isang column vector. Halimbawa

Ang mga matrice na binubuo ng isang hilera ay maaari ding isaalang-alang, halimbawa

Ang bagay na ito ay isa ring vector, ngunit row vector. Kapag nagsusuri ng data, mahalagang maunawaan kung aling mga vector ang ating kinakaharap - mga column o row. Kaya't ang spectrum na kinuha para sa isang sample ay maaaring ituring bilang isang row vector. Pagkatapos ang hanay ng mga spectral intensity sa ilang wavelength para sa lahat ng sample ay dapat ituring bilang isang column vector.

Ang dimensyon ng isang vector ay ang bilang ng mga elemento nito.

Malinaw na ang anumang column vector ay maaaring ma-transform sa isang row vector sa pamamagitan ng transposition, i.e.

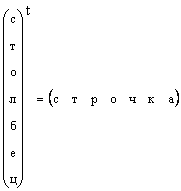
Sa mga kasong iyon kung saan ang anyo ng isang vector ay hindi partikular na tinukoy, ngunit isang vector lang ang sinabi, kung gayon ang ibig nilang sabihin ay isang column vector. Susunod din tayo sa panuntunang ito. Ang isang vector ay tinutukoy ng isang maliit na titik na direktang naka-bold na titik. Ang zero vector ay isang vector na lahat ng mga elemento ay katumbas ng zero. Ito ay ipinahiwatig 0 .

1.7. Ang pinakasimpleng operasyon na may mga vector

Ang mga vector ay maaaring idagdag at i-multiply sa mga numero sa parehong paraan tulad ng mga matrice. Halimbawa,

kanin. 13 Mga operasyon na may mga vector

Dalawang vector x at y tinawag collinear, kung may bilang na α na ganoon

1.8. Mga produkto ng mga vector

Dalawang vector ng parehong dimensyon N maaaring paramihin. Hayaang magkaroon ng dalawang vectors x = (x 1 , x 2 ,...,x N) t at y = (y 1 , y 2 ,...,y N) t . Ginagabayan ng panuntunan sa pagpaparami "hilera sa hanay", maaari tayong gumawa ng dalawang produkto mula sa mga ito: x t y at xy t . Unang gawain

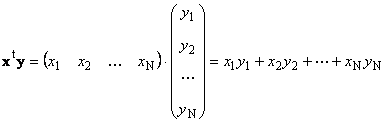
tinawag scalar o panloob. Ang resulta nito ay isang numero. Ginagamit din nito ang notasyon ( x,y)= x t y. Halimbawa,

kanin. 14 Panloob (scalar) na produkto

Pangalawang gawain

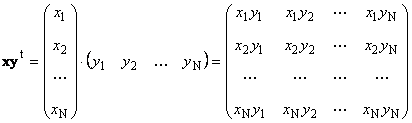
tinawag panlabas. Ang resulta nito ay isang dimension matrix ( N× N). Halimbawa,

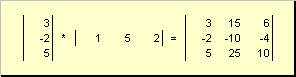
kanin. 15 Panlabas na produkto

Mga vector, produktong scalar na katumbas ng zero ay tinatawag orthogonal.

1.9. Normal na vector

Ang scalar product ng isang vector na may sarili nito ay tinatawag na scalar square. Ang halagang ito

tumutukoy sa isang parisukat haba vector x. Upang tukuyin ang haba (tinatawag ding ang nakasanayan vector) ginagamit ang notasyon

Halimbawa,

kanin. 16 Vector na pamantayan

Vector ng haba ng unit (|| x|| = 1) ay tinatawag na normalized. Nonzero vector ( x ≠ 0 ) ay maaaring gawing normal sa pamamagitan ng paghahati nito sa haba, i.e. x = ||x|| (x/||x||) = ||x|| e. Dito e = x/||x|| ay isang normalized na vector.

Ang mga vector ay tinatawag na orthonormal kung lahat sila ay normalized at pairwise orthogonal.

1.10. Anggulo sa pagitan ng mga vector

Ang scalar na produkto ay tumutukoy at iniksyonφ sa pagitan ng dalawang vector x at y

Kung ang mga vector ay orthogonal, kung gayon ang cosφ = 0 at φ = π/2, at kung sila ay collinear, kung gayon ang cosφ = 1 at φ = 0.

1.11. Vector na representasyon ng isang matrix

Ang bawat matris A laki ako× J ay maaaring kinakatawan bilang isang set ng mga vectors

Narito ang bawat vector a j ay isang j-th column at row vector b i ay isang i-ika-row ng matrix A

1.12. Mga vector na nakadepende sa linear

Mga vector ng parehong dimensyon ( N) ay maaaring idagdag at i-multiply sa isang numero, tulad ng mga matrice. Ang resulta ay isang vector ng parehong dimensyon. Hayaang magkaroon ng ilang mga vectors ng parehong dimensyon x 1 , x 2 ,...,x K at ang parehong bilang ng mga numero α α 1 , α 2 ,...,α K. Vector

y= α 1 x 1 + α 2 x 2 +...+α K x K

tinawag linear na kumbinasyon mga vector x k .

Kung mayroong mga hindi-zero na numerong α k ≠ 0, k = 1,..., K, Ano y = 0 , pagkatapos ay tulad ng isang set ng mga vectors x k tinawag nakadepende sa linear. Kung hindi, ang mga vector ay tinatawag na linearly independent. Halimbawa, mga vector x 1 = (2, 2) t at x 2 = (−1, −1) t ay linearly dependent, dahil x 1 +2x 2 = 0

1.13. Ranggo ng matrix

Isaalang-alang ang isang set ng K mga vector x 1 , x 2 ,...,x K mga sukat N. Ang ranggo ng sistemang ito ng mga vector ay ang pinakamataas na bilang ng mga linearly independent na mga vector. Halimbawa sa set

mayroon lamang dalawang linearly independent vectors, halimbawa x 1 at x 2 , kaya 2 ang ranggo nito.

Malinaw, kung mayroong higit pang mga vector sa set kaysa sa kanilang dimensyon ( K>N), kung gayon ang mga ito ay kinakailangang linearly na umaasa.

Ranggo ng matrix(tinutukoy ng ranggo( A)) ay ang ranggo ng sistema ng mga vectors na binubuo nito. Bagama't ang anumang matrix ay maaaring katawanin sa dalawang paraan (column vectors o row vectors), hindi ito nakakaapekto sa rank value, dahil

1.14. baligtad na matris

parisukat na matris A ay tinatawag na non-degenerate kung mayroon itong kakaiba reverse matris A-1 , tinutukoy ng mga kondisyon

AA −1 = A −1 A = ako.

Ang inverse matrix ay hindi umiiral para sa lahat ng matrice. Ang isang kinakailangan at sapat na kondisyon para sa hindi pagkabulok ay

det( A) ≠ 0 o ranggo( A) = N.

Ang matrix inversion ay isang kumplikadong pamamaraan kung saan mayroong mga espesyal na programa. Halimbawa,

kanin. 17 Pagbabaligtad ng matris

Nagbibigay kami ng mga formula para sa pinakasimpleng kaso - matrice 2 × 2

Kung matrices A at B ay non-degenerate, kung gayon

(AB) −1 = B −1 A −1 .

1.15. Pseudo-inverse matrix

Kung ang matris A ay degenerate at ang inverse matrix ay hindi umiiral, pagkatapos ay sa ilang mga kaso ay maaaring gamitin ng isa pseudo-inverse matrix, na tinukoy bilang tulad ng isang matrix A+ na

AA + A = A.

Ang pseudo-inverse matrix ay hindi lamang isa at ang anyo nito ay nakasalalay sa paraan ng pagtatayo. Halimbawa, para sa isang rectangular matrix, maaari mong gamitin ang Moore-Penrose method.

Kung ang bilang ng mga column ay mas mababa sa bilang ng mga row, kung gayon

A + =(A t A) −1 A t

Halimbawa,

kanin. 17a Pseudo matrix inversion

Kung ang bilang ng mga hanay mas maraming numero mga linya, pagkatapos

A + =A t ( AA t) −1

1.16. Multiplikasyon ng isang vector sa pamamagitan ng isang matrix

Vector x maaaring i-multiply sa isang matrix A angkop na sukat. Sa kasong ito, ang column vector ay pinarami sa kanan Ax, at ang vector string ay nasa kaliwa x t A. Kung ang sukat ng vector J, at ang sukat ng matrix ako× J pagkatapos ang resulta ay isang vector ng dimensyon ako. Halimbawa,

kanin. 18 Vector-Matrix Multiplication

Kung ang matris A- parisukat ( ako× ako), pagkatapos ay ang vector y = Ax ay may parehong sukat ng x. Obvious naman yun

A(α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Samakatuwid ang mga matrice ay maaaring ituring bilang mga linear na pagbabagong-anyo ng mga vectors. Sa partikular x = x, baka = 0 .

2. Karagdagang impormasyon

2.1. Mga sistema ng linear equation

Hayaan A- laki ng matrix ako× J, a b- dimensyon ng vector J. Isaalang-alang ang equation

Ax = b

may kinalaman sa vector x, mga sukat ako. Mahalaga, ito ay isang sistema ng ako linear equation na may J hindi kilala x 1 ,...,x J. Ang isang solusyon ay umiiral kung at kung lamang

ranggo( A) = ranggo( B) = R,

saan B ay ang augmented dimension matrix ako×( J+1) na binubuo ng matris A, nilagyan ng column b, B = (A b). Kung hindi, ang mga equation ay hindi pare-pareho.

Kung ang R = ako = J, kung gayon ang solusyon ay natatangi

x = A −1 b.

Kung ang R < ako, pagkatapos ay mayroong maraming iba't ibang mga solusyon na maaaring ipahayag sa mga tuntunin ng isang linear na kumbinasyon J−R mga vector. Sistema ng mga homogenous na equation Ax = 0 na may isang parisukat na matris A (N× N) ay may di-trivial na solusyon ( x ≠ 0 ) kung at kung det( A) = 0. Kung R= ranggo( A)<N, tapos meron N−R mga linearly independent na solusyon.

2.2. Bilinear at quadratic na mga anyo

Kung ang A ay isang parisukat na matris, at x at y- mga vector ng kaukulang dimensyon, pagkatapos ay ang scalar product ng form x t Ay tinawag bilinear ang hugis na tinukoy ng matrix A. Sa x = y pagpapahayag x t Ax tinawag parisukat anyo.

2.3. Positibong tiyak na matrice

parisukat na matris A tinawag positibong tiyak, kung para sa anumang nonzero vector x ≠ 0 ,

x t Ax > 0.

Ang negatibo (x t Ax < 0), hindi negatibo (x t Ax≥ 0) at hindi positibo (x t Ax≤ 0) ilang mga matrice.

2.4. Cholesky decomposition

Kung ang simetriko matrix A ay positibong tiyak, pagkatapos ay mayroong isang natatanging tatsulok na matrix U na may mga positibong elemento, kung saan

A = U t U.

Halimbawa,

kanin. 19 Cholesky decomposition

2.5. polar decomposition

Hayaan A ay isang nondegenerate square matrix ng dimensyon N× N. Tapos may kakaiba polar pagganap

A = SR,

saan S ay isang di-negatibong simetriko matrix, at R ay isang orthogonal matrix. matrice S at R maaaring malinaw na tukuyin:

S 2 = AA t o S = (AA t) ½ at R = S −1 A = (AA t) −½ A.

Halimbawa,

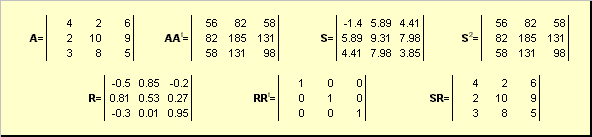
kanin. 20 Polar decomposition

Kung ang matris A ay degenerate, kung gayon ang agnas ay hindi natatangi - ibig sabihin: S mag-isa pa rin, pero R maaaring marami. Ang polar decomposition ay kumakatawan sa isang matrix A bilang kumbinasyon ng compression/stretch S at lumingon R.

2.6. Eigenvectors at eigenvalues

Hayaan A ay isang square matrix. Vector v tinawag sariling vector matrice A, kung

Av = λ v,

kung saan ang numero λ ay tinatawag eigenvalue matrice A. Kaya, ang pagbabagong-anyo na ginagawa ng matrix A higit sa vector v, ay nabawasan sa isang simpleng pag-uunat o compression na may salik na λ. Ang eigenvector ay tinutukoy hanggang sa multiplikasyon ng pare-parehong α ≠ 0, i.e. kung v ay isang eigenvector, pagkatapos ay α v ay isa ring eigenvector.

2.7. Eigenvalues

Sa matrix A, sukat ( N× N) ay hindi maaaring mas malaki kaysa sa N eigenvalues. Nabusog sila katangian equation

det( A − λ ako) = 0,

pagiging algebraic equation N-ika-utos. Sa partikular, para sa isang 2×2 matrix, ang katangiang equation ay may anyo

Halimbawa,

kanin. 21 Eigenvalues

Set ng eigenvalues λ 1 ,..., λ N matrice A tinawag spectrum A.

Ang spectrum ay may iba't ibang katangian. Sa partikular

det( A) = λ 1×...×λ N, Sp( A) = λ 1 +...+λ N.

Ang eigenvalues ng isang arbitrary na matrix ay maaaring kumplikadong mga numero, ngunit kung ang matrix ay simetriko ( A t = A), kung gayon ang mga eigenvalues nito ay totoo.

2.8. Mga Eigenvector

Sa matrix A, sukat ( N× N) ay hindi maaaring mas malaki kaysa sa N eigenvectors, bawat isa ay tumutugma sa sarili nitong halaga. Upang matukoy ang eigenvector v n kailangan mong lutasin ang isang sistema ng mga homogenous na equation

(A − λ n ako)v n = 0 .

Mayroon itong di-maliit na solusyon dahil det( a-λ n ako) = 0.

Halimbawa,

kanin. 22 Eigenvectors

Ang eigenvectors ng isang simetriko matrix ay orthogonal.

Eigenvalues (mga numero) at eigenvectors.
Mga halimbawa ng solusyon

Maging sarili mo

Mula sa parehong mga equation ito ay sumusunod na .

Ilagay natin pagkatapos: .

Ang resulta: ay ang pangalawang eigenvector.

Ulitin natin mahahalagang puntos mga solusyon:

– tiyak na mayroon ang resultang sistema karaniwang desisyon(ang mga equation ay linearly dependent);

- Ang "Y" ay pinili sa paraang ito ay integer at ang unang "x" na coordinate ay integer, positibo at maliit hangga't maaari.

– sinusuri namin na ang partikular na solusyon ay nakakatugon sa bawat equation ng system.

Sagot .

Ang mga intermediate na "checkpoints" ay sapat na, kaya ang pagsusuri ng mga pagkakapantay-pantay, sa prinsipyo, ay kalabisan.

AT iba't ibang mga mapagkukunan impormasyon, ang mga coordinate ng eigenvectors ay madalas na nakasulat hindi sa mga haligi, ngunit sa mga hilera, halimbawa: (at, sa totoo lang, ako mismo ang sumulat ng mga ito sa mga linya). Ang pagpipiliang ito ay katanggap-tanggap, ngunit sa liwanag ng paksa mga linear na pagbabago teknikal na mas maginhawang gamitin mga vector ng haligi.

Marahil ang solusyon ay tila napakatagal sa iyo, ngunit iyon ay dahil nagkomento ako sa unang halimbawa nang detalyado.

Halimbawa 2

matrice

Nagsasanay kami sa aming sarili! Isang tinatayang sample ng huling disenyo ng gawain sa pagtatapos ng aralin.

Minsan kailangan mong magsagawa ng karagdagang gawain, lalo na:

isulat ang canonical decomposition ng matrix

Ano ito?

Kung nabuo ang matrix eigenvectors batayan, pagkatapos ay maaari itong katawanin bilang:

Nasaan ang isang matrix na binubuo ng mga coordinate ng eigenvectors, - dayagonal matrix na may kaukulang mga eigenvalues.

Ang matrix decomposition na ito ay tinatawag kanonikal o dayagonal.

Isaalang-alang ang matrix ng unang halimbawa. Ang kanyang sariling mga vectors linearly independent(non-collinear) at bumubuo ng batayan. Gumawa tayo ng isang matrix mula sa kanilang mga coordinate:

Sa pangunahing dayagonal matrice sa angkop na kaayusan Ang mga eigenvalues ay matatagpuan, at ang natitirang mga elemento ay katumbas ng zero:
- muli kong binibigyang-diin ang kahalagahan ng pagkakasunud-sunod: "dalawa" ay tumutugma sa 1st vector at samakatuwid ay matatagpuan sa 1st column, "three" - sa 2nd vector.

Ayon sa karaniwang algorithm para sa paghahanap baligtad na matris o Gauss-Jordan na pamamaraan hanapin . Hindi, hindi iyon isang typo! - sa harap mo ay bihira, tulad ng solar eclipse kaganapan kapag ang inverse ay tumugma sa orihinal na matrix.

Nananatili itong isulat ang canonical decomposition ng matrix :

Ang sistema ay maaaring malutas gamit ang elementarya na pagbabago at sa mga sumusunod na halimbawa ay gagamitin natin ang pamamaraang ito. Ngunit narito ang paraan ng "paaralan" ay gumagana nang mas mabilis. Mula sa ika-3 equation ipinapahayag namin: - palitan sa pangalawang equation:

Dahil ang unang coordinate ay zero, nakakakuha tayo ng isang sistema , mula sa bawat equation kung saan sinusundan nito iyon .

At muli bigyang-pansin ang ipinag-uutos na presensya ng isang linear na relasyon. Kung puro solusyon lang ang makukuha , pagkatapos ay ang eigenvalue ay natagpuan nang hindi tama, o ang system ay pinagsama / nalutas na may isang error.

Ang mga compact na coordinate ay nagbibigay ng halaga

Eigenvector:

At muli, sinusuri namin na ang nahanap na solusyon natutugunan ang bawat equation ng system. Sa mga sumusunod na talata at sa mga kasunod na gawain, inirerekumenda ko na ang hiling na ito ay tanggapin bilang isang ipinag-uutos na tuntunin.

2) Para sa eigenvalue, na sumusunod sa parehong prinsipyo, nakukuha namin ang sumusunod na sistema:

Mula sa 2nd equation ng system na ipinapahayag namin: - palitan sa ikatlong equation:

Dahil ang "Z" coordinate ay katumbas ng zero, nakakakuha kami ng isang system , mula sa bawat equation kung saan sumusunod ang isang linear dependence.

Hayaan

Sinusuri namin na ang solusyon natutugunan ang bawat equation ng system.

Kaya, ang eigenvector: .

3) At, sa wakas, ang sistema ay tumutugma sa sarili nitong halaga:

Ang pangalawang equation ay mukhang pinakasimple, kaya ipinapahayag namin ito mula dito at pinapalitan ito sa 1st at 3rd equation:

Maayos ang lahat - ipinakita ang isang linear na pag-asa, na pinapalitan namin sa expression:

Bilang resulta, ang "X" at "Y" ay ipinahayag sa pamamagitan ng "Z": . Sa pagsasagawa, hindi kinakailangan na makamit lamang ang gayong mga relasyon; sa ilang mga kaso ay mas maginhawang ipahayag ang parehong sa pamamagitan ng o at sa pamamagitan ng . O kahit isang "tren" - halimbawa, "X" hanggang "Y", at "Y" hanggang "Z"

Ilagay natin pagkatapos:

Sinusuri namin na ang nahanap na solusyon natutugunan ang bawat equation ng system at isulat ang ikatlong eigenvector

Sagot: eigenvectors:

Sa geometriko, tinutukoy ng mga vector na ito ang tatlong magkakaibang spatial na direksyon ("Ayan at babalik ulit"), Ayon sa linear na pagbabago binabago ang mga nonzero vectors (eigenvectors) sa mga vector na magkakatulad sa kanila.

Kung sa pamamagitan ng kundisyon ay kinakailangan upang makahanap ng isang kanonikal na pagpapalawak ng , kung gayon ito ay posible dito, dahil iba't ibang eigenvalues ay tumutugma sa iba't ibang linearly independent eigenvectors. Gumagawa kami ng matrix mula sa kanilang mga coordinate, ang diagonal matrix mula sa kaugnay eigenvalues at hanapin baligtad na matris .

Kung, ayon sa kondisyon, kailangang magsulat linear transformation matrix sa batayan ng eigenvectors, pagkatapos ay ibibigay namin ang sagot sa form . Mayroong pagkakaiba, at isang makabuluhang pagkakaiba! Para sa matrix na ito ay ang matrix na "de".

Isang problema sa mas simpleng mga kalkulasyon para sa malayang desisyon:

Halimbawa 5

Maghanap ng mga eigenvector ng linear transformation na ibinigay ng matrix

Kapag naghahanap ng sarili mong mga numero, subukang huwag dalhin ang case sa isang polynomial ng 3rd degree. Bilang karagdagan, ang iyong mga solusyon sa system ay maaaring naiiba sa aking mga solusyon - walang malinaw dito; at ang mga vector na makikita mo ay maaaring magkaiba mula sa mga sample na vector hanggang sa proporsyonalidad sa kani-kanilang mga coordinate. Halimbawa, at . Ito ay mas aesthetically nakalulugod upang ipakita ang sagot sa anyo ng , ngunit ito ay okay kung titigil ka sa pangalawang opsyon. Gayunpaman, may mga makatwirang limitasyon sa lahat, ang bersyon ay hindi na mukhang napakahusay.

Isang tinatayang huling sample ng takdang-aralin sa pagtatapos ng aralin.

Paano malutas ang problema sa kaso ng maraming eigenvalues?

Ang pangkalahatang algorithm ay nananatiling pareho, ngunit mayroon itong sariling mga kakaiba, at ipinapayong panatilihin ang ilang mga seksyon ng solusyon sa isang mas mahigpit na istilong pang-akademiko:

Halimbawa 6

Maghanap ng mga eigenvalues at eigenvectors

Desisyon

Siyempre, i-capitalize natin ang kamangha-manghang unang column:

At, pagkatapos i-factor ang square trinomial:

Bilang isang resulta, ang mga eigenvalues ay nakuha, dalawa sa mga ito ay multiple.

Hanapin natin ang eigenvectors:

1) Haharapin natin ang isang nag-iisang sundalo ayon sa isang "pinasimple" na pamamaraan:

Mula sa huling dalawang equation, ang pagkakapantay-pantay ay malinaw na nakikita, na, malinaw naman, ay dapat ipalit sa 1st equation ng system:

Walang mas mahusay na kumbinasyon:
Eigenvector:

2-3) Ngayon ay tinanggal namin ang isang pares ng mga bantay. Sa kasong ito, maaaring ito ay dalawa man o isa eigenvector. Anuman ang multiplicity ng mga ugat, pinapalitan namin ang halaga sa determinant , na nagdadala sa amin ng mga sumusunod homogenous na sistema ng mga linear na equation:

Ang mga eigenvector ay eksaktong mga vector
pangunahing sistema ng pagpapasya

Sa totoo lang, sa buong aralin, kami ay nakatuon lamang sa paghahanap ng mga vectors ng pangunahing sistema. Sa ngayon, ang terminong ito ay hindi partikular na kinakailangan. Siyanga pala, iyong mga matatalino na estudyante na, naka-camouflage homogenous equation, ay mapipilitang manigarilyo ngayon.

iisang aksyon ay upang alisin ang mga karagdagang linya. Ang resulta ay isang "isa sa tatlong" matrix na may pormal na "hakbang" sa gitna.
– pangunahing variable, – libreng variable. Mayroong dalawang libreng variable, kaya mayroon ding dalawang vectors ng pangunahing sistema.

Ipahayag natin ang pangunahing variable sa mga tuntunin ng mga libreng variable: . Ang zero factor sa harap ng "x" ay nagbibigay-daan dito na kumuha ng ganap na anumang mga halaga (na malinaw din na nakikita mula sa sistema ng mga equation).

Sa konteksto ng problemang ito, mas maginhawang isulat ang pangkalahatang solusyon hindi sa isang hilera, ngunit sa isang haligi:

Ang pares ay tumutugma sa isang eigenvector:
Ang pares ay tumutugma sa isang eigenvector:

Tandaan : maaaring kunin ng mga sopistikadong mambabasa ang mga vector na ito nang pasalita - sa pamamagitan lamang ng pagsusuri sa system , ngunit kailangan ang ilang kaalaman dito: mayroong tatlong variable, ranggo ng system matrix- ibig sabihin ng unit pangunahing sistema ng pagpapasya binubuo ng 3 – 1 = 2 vectors. Gayunpaman, ang mga nahanap na vector ay perpektong nakikita kahit na walang kaalaman na ito, puro sa isang intuitive na antas. Sa kasong ito, ang ikatlong vector ay isusulat nang "mas maganda": . Gayunpaman, binabalaan kita, sa isa pang halimbawa, maaaring walang simpleng pagpili, kaya naman ang reserbasyon ay inilaan para sa mga taong may karanasan. Bukod, bakit hindi kunin bilang ikatlong vector, sabihin nating, ? Pagkatapos ng lahat, ang mga coordinate nito ay nagbibigay-kasiyahan din sa bawat equation ng system, at ang mga vectors ay linearly independent. Ang pagpipiliang ito, sa prinsipyo, ay angkop, ngunit "baluktot", dahil ang "iba pang" vector ay isang linear na kumbinasyon ng mga vector ng pangunahing sistema.

Sagot: eigenvalues: , eigenvectors:

Isang katulad na halimbawa para sa isang do-it-yourself na solusyon:

Halimbawa 7

Maghanap ng mga eigenvalues at eigenvectors

Isang tinatayang sample ng pagtatapos sa pagtatapos ng aralin.

Dapat pansinin na sa parehong ika-6 at ika-7 na halimbawa, isang triple ng mga linearly independent na eigenvectors ang nakuha, at samakatuwid ang orihinal na matrix ay maaaring katawanin sa canonical expansion . Ngunit ang gayong mga raspberry ay hindi nangyayari sa lahat ng mga kaso:

Halimbawa 8

Desisyon: buuin at lutasin ang katangiang equation:

Pinapalawak namin ang determinant sa pamamagitan ng unang column:

Nagsasagawa kami ng mga karagdagang pagpapasimple ayon sa isinasaalang-alang na pamamaraan, pag-iwas sa isang polynomial ng 3rd degree:

ay mga eigenvalues.