How to solve quadratic equations with large numbers. Finding the discriminant, formula, comparison with zero

Consider the quadratic equation:
(1) .
The roots of a quadratic equation(1) are determined by the formulas:
; .
These formulas can be combined like this:
.
When the roots of the quadratic equation are known, then the polynomial of the second degree can be represented as a product of factors (factored):
.

Further, we assume that are real numbers.
Consider discriminant of a quadratic equation:
.
If the discriminant is positive, then the quadratic equation (1) has two different real roots:
; .
Then the factorization of the square trinomial has the form:
.
If the discriminant is zero, then the quadratic equation (1) has two multiple (equal) real roots:
.
Factorization:
.
If the discriminant is negative, then the quadratic equation (1) has two complex conjugate roots:
;
.
Here is the imaginary unit, ;
and are the real and imaginary parts of the roots:
; .
Then

.

Graphic interpretation

If build function graph
,
which is a parabola, then the points of intersection of the graph with the axis will be the roots of the equation
.
When , the graph intersects the abscissa axis (axis) at two points.
When , the graph touches the x-axis at one point.
When , the graph does not cross the x-axis.

Below are examples of such graphs.

Useful Formulas Related to Quadratic Equation

(f.1) ;
(f.2) ;
(f.3) .

Derivation of the formula for the roots of a quadratic equation

We perform transformations and apply formulas (f.1) and (f.3):




,
where
; .

So, we got the formula for the polynomial of the second degree in the form:
.
From this it can be seen that the equation

performed at
And .
That is, and are the roots of the quadratic equation
.

Examples of determining the roots of a quadratic equation

Example 1

(1.1) .

Solution

.
Comparing with our equation (1.1), we find the values ​​of the coefficients:
.
Finding the discriminant:
.
Since the discriminant is positive, the equation has two real roots:
;
;
.

From here we obtain the decomposition of the square trinomial into factors:

.

Graph of the function y = 2 x 2 + 7 x + 3 crosses the x-axis at two points.

Let's plot the function
.
The graph of this function is a parabola. It crosses the x-axis (axis) at two points:
And .
These points are the roots of the original equation (1.1).

Answer

;
;
.

Example 2

Find the roots of a quadratic equation:
(2.1) .

Solution

We write the quadratic equation in general view:
.
Comparing with the original equation (2.1), we find the values ​​of the coefficients:
.
Finding the discriminant:
.
Since the discriminant is zero, the equation has two multiple (equal) roots:
;
.

Then the factorization of the trinomial has the form:
.

Graph of the function y = x 2 - 4 x + 4 touches the x-axis at one point.

Let's plot the function
.
The graph of this function is a parabola. It touches the x-axis (axis) at one point:
.
This point is the root of the original equation (2.1). Since this root is factored twice:
,
then such a root is called a multiple. That is, they consider that there are two equal roots:
.

Answer

;
.

Example 3

Find the roots of a quadratic equation:
(3.1) .

Solution

We write the quadratic equation in general form:
(1) .
Let us rewrite the original equation (3.1):
.
Comparing with (1), we find the values ​​of the coefficients:
.
Finding the discriminant:
.
The discriminant is negative, . Therefore, there are no real roots.

You can find complex roots:
;
;

Let's plot the function
.
The graph of this function is a parabola. It does not cross the abscissa (axis). Therefore, there are no real roots.

Answer

There are no real roots. Complex roots:
;
;
.

With this math program you can solve quadratic equation.

The program not only gives the answer to the problem, but also displays the solution process in two ways:
- using the discriminant
- using the Vieta theorem (if possible).

Moreover, the answer is displayed exact, not approximate.
For example, for the equation \(81x^2-16x-1=0\), the answer is displayed in this form:

This program May be useful for high school students general education schools in preparation for control work and exams, when testing knowledge before the exam, parents to control the solution of many problems in mathematics and algebra. Or maybe it's too expensive for you to hire a tutor or buy new textbooks? Or do you just want to get it done as soon as possible? homework math or algebra? In this case, you can also use our programs with a detailed solution.

In this way, you can conduct your own training and/or the training of your younger brothers or sisters, while the level of education in the field of tasks to be solved is increased.

If you are not familiar with the rules for entering a square polynomial, we recommend that you familiarize yourself with them.

Rules for entering a square polynomial

Any Latin letter can act as a variable.
For example: \(x, y, z, a, b, c, o, p, q \) etc.

Numbers can be entered as integers or fractions.
Moreover, fractional numbers can be entered not only in the form of a decimal, but also in the form of an ordinary fraction.

Rules for entering decimal fractions.
In decimal fractions, the fractional part from the integer can be separated by either a dot or a comma.
For example, you can enter decimals so: 2.5x - 3.5x^2

Rules for entering ordinary fractions.
Only a whole number can act as the numerator, denominator and integer part of a fraction.

The denominator cannot be negative.

When entering a numerical fraction, the numerator is separated from the denominator by a division sign: /
whole part separated from the fraction by an ampersand: &
Input: 3&1/3 - 5&6/5z +1/7z^2
Result: \(3\frac(1)(3) - 5\frac(6)(5) z + \frac(1)(7)z^2 \)

When entering an expression you can use brackets. In this case, when solving a quadratic equation, the introduced expression is first simplified.
For example: 1/2(y-1)(y+1)-(5y-10&1/2)

It was found that some scripts needed to solve this task were not loaded, and the program may not work.
You may have AdBlock enabled.
In this case, disable it and refresh the page.

Because There are a lot of people who want to solve the problem, your request is queued.
After a few seconds, the solution will appear below.
Please wait sec...

If you noticed an error in the solution, then you can write about it in the Feedback Form .
Do not forget indicate which task you decide what enter in the fields.

Our games, puzzles, emulators:

A bit of theory.

Quadratic equation and its roots. Incomplete quadratic equations

Each of the equations
\(-x^2+6x+1,4=0, \quad 8x^2-7x=0, \quad x^2-\frac(4)(9)=0 \)
has the form
\(ax^2+bx+c=0, \)
where x is a variable, a, b and c are numbers.
In the first equation a = -1, b = 6 and c = 1.4, in the second a = 8, b = -7 and c = 0, in the third a = 1, b = 0 and c = 4/9. Such equations are called quadratic equations.

Definition.
quadratic equation an equation of the form ax 2 +bx+c=0 is called, where x is a variable, a, b and c are some numbers, and \(a \neq 0 \).

The numbers a, b and c are the coefficients of the quadratic equation. The number a is called the first coefficient, the number b is the second coefficient and the number c is the intercept.

In each of the equations of the form ax 2 +bx+c=0, where \(a \neq 0 \), the largest power of the variable x is a square. Hence the name: quadratic equation.

Note that a quadratic equation is also called an equation of the second degree, since its left side is a polynomial of the second degree.

A quadratic equation in which the coefficient at x 2 is 1 is called reduced quadratic equation. For example, the given quadratic equations are the equations
\(x^2-11x+30=0, \quad x^2-6x=0, \quad x^2-8=0 \)

If in the quadratic equation ax 2 +bx+c=0 at least one of the coefficients b or c is equal to zero, then such an equation is called incomplete quadratic equation. So, the equations -2x 2 +7=0, 3x 2 -10x=0, -4x 2 =0 are incomplete quadratic equations. In the first of them b=0, in the second c=0, in the third b=0 and c=0.

Incomplete quadratic equations are of three types:
1) ax 2 +c=0, where \(c \neq 0 \);
2) ax 2 +bx=0, where \(b \neq 0 \);
3) ax2=0.

Consider the solution of equations of each of these types.

To solve an incomplete quadratic equation of the form ax 2 +c=0 for \(c \neq 0 \), its free term is transferred to right side and divide both sides of the equation by a:
\(x^2 = -\frac(c)(a) \Rightarrow x_(1,2) = \pm \sqrt( -\frac(c)(a)) \)

Since \(c \neq 0 \), then \(-\frac(c)(a) \neq 0 \)

If \(-\frac(c)(a)>0 \), then the equation has two roots.

If \(-\frac(c)(a) To solve an incomplete quadratic equation of the form ax 2 +bx=0 for \(b \neq 0 \) factorize its left side and obtain the equation
\(x(ax+b)=0 \Rightarrow \left\( \begin(array)(l) x=0 \\ ax+b=0 \end(array) \right. \Rightarrow \left\( \begin (array)(l) x=0 \\ x=-\frac(b)(a) \end(array) \right. \)

Hence, an incomplete quadratic equation of the form ax 2 +bx=0 for \(b \neq 0 \) always has two roots.

An incomplete quadratic equation of the form ax 2 \u003d 0 is equivalent to the equation x 2 \u003d 0 and therefore has a single root 0.

The formula for the roots of a quadratic equation

Let us now consider how quadratic equations are solved in which both coefficients of the unknowns and the free term are nonzero.

We solve the quadratic equation in general form and as a result we obtain the formula of the roots. Then this formula can be applied to solve any quadratic equation.

Solve the quadratic equation ax 2 +bx+c=0

Dividing both its parts by a, we obtain the equivalent reduced quadratic equation
\(x^2+\frac(b)(a)x +\frac(c)(a)=0 \)

We transform this equation by highlighting the square of the binomial:
\(x^2+2x \cdot \frac(b)(2a)+\left(\frac(b)(2a)\right)^2- \left(\frac(b)(2a)\right)^ 2 + \frac(c)(a) = 0 \Rightarrow \)

The root expression is called discriminant of a quadratic equation ax 2 +bx+c=0 (“discriminant” in Latin - distinguisher). It is denoted by the letter D, i.e.
\(D = b^2-4ac\)

Now, using the notation of the discriminant, we rewrite the formula for the roots of the quadratic equation:
\(x_(1,2) = \frac( -b \pm \sqrt(D) )(2a) \), where \(D= b^2-4ac \)

It's obvious that:
1) If D>0, then the quadratic equation has two roots.
2) If D=0, then the quadratic equation has one root \(x=-\frac(b)(2a)\).
3) If D Thus, depending on the value of the discriminant, the quadratic equation can have two roots (for D > 0), one root (for D = 0) or no roots (for D When solving a quadratic equation using this formula, it is advisable to do the following way:
1) calculate the discriminant and compare it with zero;
2) if the discriminant is positive or equal to zero, then use the root formula, if the discriminant is negative, then write down that there are no roots.

Vieta's theorem

The given quadratic equation ax 2 -7x+10=0 has roots 2 and 5. The sum of the roots is 7, and the product is 10. We see that the sum of the roots is equal to the second coefficient, taken with the opposite sign, and the product of the roots is equal to the free term. Any reduced quadratic equation that has roots has this property.

The sum of the roots of the given quadratic equation is equal to the second coefficient, taken with the opposite sign, and the product of the roots is equal to the free term.

Those. Vieta's theorem states that the roots x 1 and x 2 of the reduced quadratic equation x 2 +px+q=0 have the property:
\(\left\( \begin(array)(l) x_1+x_2=-p \\ x_1 \cdot x_2=q \end(array) \right. \)

Quadratic equation - easy to solve! *Further in the text "KU". Friends, it would seem that in mathematics it can be easier than solving such an equation. But something told me that many people have problems with him. I decided to see how many impressions Yandex gives per request per month. Here's what happened, take a look:

What does it mean? This means that about 70,000 people a month are looking for this information, what does this summer have to do with it, and what will be among school year- requests will be twice as large. This is not surprising, because those guys and girls who have long graduated from school and are preparing for the exam are looking for this information, and schoolchildren are also trying to refresh their memory.

Despite the fact that there are a lot of sites that tell how to solve this equation, I decided to also contribute and publish the material. Firstly, I want visitors to come to my site on this request; secondly, in other articles, when the speech “KU” comes up, I will give a link to this article; thirdly, I will tell you a little more about his solution than is usually stated on other sites. Let's get started! The content of the article:

A quadratic equation is an equation of the form:

where coefficients a,band with arbitrary numbers, with a≠0.

In the school course, the material is given in the following form - the division of equations into three classes is conditionally done:

1. Have two roots.

2. * Have only one root.

3. Have no roots. It is worth noting here that they do not have real roots

How are roots calculated? Just!

We calculate the discriminant. Under this "terrible" word lies a very simple formula:

The root formulas are as follows:

*These formulas must be known by heart.

You can immediately write down and solve:

Example:

1. If D > 0, then the equation has two roots.

2. If D = 0, then the equation has one root.

3. If D< 0, то уравнение не имеет действительных корней.

Let's look at the equation:

On this occasion, when the discriminant is zero, the school course says that one root is obtained, here it is equal to nine. That's right, it is, but...

This representation is somewhat incorrect. In fact, there are two roots. Yes, yes, do not be surprised, it turns out two equal roots, and to be mathematically accurate, then two roots should be written in the answer:

x 1 = 3 x 2 = 3

But this is so - a small digression. At school, you can write down and say that there is only one root.

Now the following example:

As we know, the root of negative number is not extracted, so there is no solution in this case.

That's the whole decision process.

Quadratic function.

Here is how the solution looks geometrically. This is extremely important to understand (in the future, in one of the articles, we will analyze in detail the solution of a quadratic inequality).

This is a function of the form:

where x and y are variables

a, b, c are given numbers, where a ≠ 0

The graph is a parabola:

That is, it turns out that solving the quadratic equation with "y" zero we find the points of intersection of the parabola with the x-axis. There can be two of these points (the discriminant is positive), one (the discriminant is zero) or none (the discriminant is negative). Details about quadratic function You can view article by Inna Feldman.

Consider examples:

Example 1: Decide 2x 2 +8 x–192=0

a=2 b=8 c= -192

D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Answer: x 1 = 8 x 2 = -12

* You could immediately divide the left and right sides of the equation by 2, that is, simplify it. The calculations will be easier.

Example 2: Solve x2–22 x+121 = 0

a=1 b=-22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

We got that x 1 \u003d 11 and x 2 \u003d 11

In the answer, it is permissible to write x = 11.

Answer: x = 11

Example 3: Solve x 2 –8x+72 = 0

a=1 b= -8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

The discriminant is negative, there is no solution in real numbers.

Answer: no solution

The discriminant is negative. There is a solution!

Here we will talk about solving the equation in the case when it turns out negative discriminant. Do you know anything about complex numbers? I will not go into detail here about why and where they arose and what their specific role and necessity in mathematics is, this is a topic for a large separate article.

The concept of a complex number.

A bit of theory.

A complex number z is a number of the form

z = a + bi

where a and b are real numbers, i is the so-called imaginary unit.

a+bi is a SINGLE NUMBER, not an addition.

The imaginary unit is equal to the root of minus one:

Now consider the equation:

Get two conjugate roots.

Incomplete quadratic equation.

Consider special cases, this is when the coefficient "b" or "c" is equal to zero (or both are equal to zero). They are solved easily without any discriminants.

Case 1. Coefficient b = 0.

The equation takes the form:

Let's transform:

Example:

4x 2 -16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = -2

Case 2. Coefficient c = 0.

The equation takes the form:

Transform, factorize:

*The product is equal to zero when at least one of the factors is equal to zero.

Example:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 or x–5 =0

x 1 = 0 x 2 = 5

Case 3. Coefficients b = 0 and c = 0.

Here it is clear that the solution to the equation will always be x = 0.

Useful properties and patterns of coefficients.

There are properties that allow solving equations with large coefficients.

butx 2 + bx+ c=0 equality

a + b+ c = 0, then

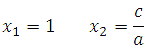
— if for the coefficients of the equation butx 2 + bx+ c=0 equality

a+ with =b, then

These properties help to a certain kind equations.

Example 1: 5001 x 2 –4995 x – 6=0

The sum of the coefficients is 5001+( – 4995)+(– 6) = 0, so

Example 2: 2501 x 2 +2507 x+6=0

Equality a+ with =b, means

Regularities of coefficients.

1. If in the equation ax 2 + bx + c \u003d 0 the coefficient "b" is (a 2 +1), and the coefficient "c" is numerically equal to the coefficient "a", then its roots are

ax 2 + (a 2 +1) ∙ x + a \u003d 0 \u003d\u003e x 1 \u003d -a x 2 \u003d -1 / a.

Example. Consider the equation 6x 2 +37x+6 = 0.

x 1 \u003d -6 x 2 \u003d -1/6.

2. If in the equation ax 2 - bx + c \u003d 0, the coefficient "b" is (a 2 +1), and the coefficient "c" is numerically equal to the coefficient "a", then its roots are

ax 2 - (a 2 + 1) ∙ x + a \u003d 0 \u003d\u003e x 1 \u003d a x 2 \u003d 1 / a.

Example. Consider the equation 15x 2 –226x +15 = 0.

x 1 = 15 x 2 = 1/15.

3. If in the equation ax 2 + bx - c = 0 coefficient "b" equals (a 2 – 1), and the coefficient “c” numerically equal to the coefficient "a", then its roots are equal

ax 2 + (a 2 -1) ∙ x - a \u003d 0 \u003d\u003e x 1 \u003d - a x 2 \u003d 1 / a.

Example. Consider the equation 17x 2 + 288x - 17 = 0.

x 1 \u003d - 17 x 2 \u003d 1/17.

4. If in the equation ax 2 - bx - c \u003d 0, the coefficient "b" is equal to (a 2 - 1), and the coefficient c is numerically equal to the coefficient "a", then its roots are

ax 2 - (a 2 -1) ∙ x - a \u003d 0 \u003d\u003e x 1 \u003d a x 2 \u003d - 1 / a.

Example. Consider the equation 10x2 - 99x -10 = 0.

x 1 \u003d 10 x 2 \u003d - 1/10

Vieta's theorem.

Vieta's theorem is named after the famous French mathematician Francois Vieta. Using Vieta's theorem, one can express the sum and product of the roots of an arbitrary KU in terms of its coefficients.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

In sum, the number 14 gives only 5 and 9. These are the roots. With a certain skill, using the presented theorem, you can solve many quadratic equations immediately orally.

Vieta's theorem, moreover. convenient because after solving the quadratic equation in the usual way (through the discriminant), the resulting roots can be checked. I recommend doing this all the time.

TRANSFER METHOD

With this method, the coefficient "a" is multiplied by the free term, as if "transferred" to it, which is why it is called transfer method. This method is used when it is easy to find the roots of an equation using Vieta's theorem and, most importantly, when the discriminant is an exact square.

If but± b+c≠ 0, then the transfer technique is used, for example:

2X 2 – 11x+ 5 = 0 (1) => X 2 – 11x+ 10 = 0 (2)

According to the Vieta theorem in equation (2), it is easy to determine that x 1 \u003d 10 x 2 \u003d 1

The obtained roots of the equation must be divided by 2 (since the two were “thrown” from x 2), we get

x 1 \u003d 5 x 2 \u003d 0.5.

What is the rationale? See what's happening.

The discriminants of equations (1) and (2) are:

If you look at the roots of the equations, then only different denominators are obtained, and the result depends precisely on the coefficient at x 2:

The second (modified) roots are 2 times larger.

Therefore, we divide the result by 2.

*If we roll three of a kind, then we divide the result by 3, and so on.

Answer: x 1 = 5 x 2 = 0.5

sq. ur-ie and the exam.

I will say briefly about its importance - YOU SHOULD BE ABLE TO DECIDE quickly and without thinking, you need to know the formulas of the roots and the discriminant by heart. A lot of the tasks that are part of the USE tasks come down to solving a quadratic equation (including geometric ones).

What is worth noting!

1. The form of the equation can be "implicit". For example, the following entry is possible:

15+ 9x 2 - 45x = 0 or 15x+42+9x 2 - 45x=0 or 15 -5x+10x 2 = 0.

You need to bring him to standard view(so as not to get confused when deciding).

2. Remember that x is an unknown value and it can be denoted by any other letter - t, q, p, h and others.

For example, for the trinomial \(3x^2+2x-7\), the discriminant will be \(2^2-4\cdot3\cdot(-7)=4+84=88\). And for the trinomial \(x^2-5x+11\), it will be equal to \((-5)^2-4\cdot1\cdot11=25-44=-19\).

The discriminant is denoted by the letter \(D\) and is often used when solving. Also, by the value of the discriminant, you can understand what the graph looks like (see below).

Discriminant and roots of the quadratic equation

The value of the discriminant shows the amount of the quadratic equation:
- if \(D\) is positive, the equation will have two roots;
- if \(D\) is equal to zero - only one root;
- if \(D\) is negative, there are no roots.

This does not need to be taught, it is easy to come to such a conclusion, simply knowing that from the discriminant (that is, \(\sqrt(D)\) is included in the formula for calculating the roots of the quadratic equation: \(x_(1)=\)\( \frac(-b+\sqrt(D))(2a)\) and \(x_(2)=\)\(\frac(-b-\sqrt(D))(2a)\) Let's look at each case more.

If the discriminant is positive

In this case, the root of it is some positive number, which means \(x_(1)\) and \(x_(2)\) will be different in value, because in the first formula \(\sqrt(D)\) is added, and in the second it is subtracted. And we have two different roots.

Example : Find the roots of the equation \(x^2+2x-3=0\)
Solution :

Answer : \(x_(1)=1\); \(x_(2)=-3\)

If the discriminant is zero

And how many roots will there be if the discriminant is zero? Let's reason.

The root formulas look like this: \(x_(1)=\)\(\frac(-b+\sqrt(D))(2a)\) and \(x_(2)=\)\(\frac(-b- \sqrt(D))(2a)\) . And if the discriminant is zero, then the root of it is also zero. Then it turns out:

\(x_(1)=\)\(\frac(-b+\sqrt(D))(2a)\) \(=\)\(\frac(-b+\sqrt(0))(2a)\) \(=\)\(\frac(-b+0)(2a)\) \(=\)\(\frac(-b)(2a)\)

\(x_(2)=\)\(\frac(-b-\sqrt(D))(2a)\) \(=\)\(\frac(-b-\sqrt(0))(2a) \) \(=\)\(\frac(-b-0)(2a)\) \(=\)\(\frac(-b)(2a)\)

That is, the values ​​of the roots of the equation will match, because adding or subtracting zero does not change anything.

Example : Find the roots of the equation \(x^2-4x+4=0\)
Solution :

Answer : \(x=2\)

The use of equations is widespread in our lives. They are used in many calculations, construction of structures and even sports. Equations have been used by man since ancient times and since then their use has only increased. The discriminant allows you to solve any quadratic equations using general formula, which has the following form:

The discriminant formula depends on the degree of the polynomial. The above formula is suitable for solving quadratic equations of the following form:

The discriminant has the following properties that you need to know:

* "D" is 0 when the polynomial has multiple roots (equal roots);

* "D" is a symmetric polynomial with respect to the roots of the polynomial and therefore is a polynomial in its coefficients; moreover, the coefficients of this polynomial are integers, regardless of the extension in which the roots are taken.

Suppose we are given a quadratic equation of the following form:

1 equation

According to the formula we have:

Since \, then the equation has 2 roots. Let's define them:

Where can I solve the equation through the discriminant online solver?

You can solve the equation on our website https: // site. Free online solver will allow you to solve an online equation of any complexity in seconds. All you have to do is just enter your data into the solver. You can also watch the video instruction and learn how to solve the equation on our website. And if you have any questions, you can ask them in our Vkontakte group http://vk.com/pocketteacher. Join our group, we are always happy to help you.