Isulat ang canonical equation ng ellipse. Mga kurba ng pangalawang pagkakasunud-sunod
Kahulugan 7.1. Ang hanay ng lahat ng mga punto sa eroplano kung saan ang kabuuan ng mga distansya sa dalawang nakapirming puntos na F 1 at F 2 ay isang ibinigay na pare-pareho ay tinatawag na ellipse.
Ang kahulugan ng isang ellipse ay nagbibigay ng sumusunod na paraan ng pagbuo nito sa geometrically. Inaayos namin ang dalawang puntos na F 1 at F 2 sa eroplano, at tinutukoy ang isang di-negatibong pare-parehong halaga ng 2a. Hayaan ang distansya sa pagitan ng mga punto F 1 at F 2 ay katumbas ng 2c. Isipin na ang isang hindi mapalawak na thread ng haba 2a ay naayos sa mga punto F 1 at F 2, halimbawa, sa tulong ng dalawang karayom. Malinaw na ito ay posible lamang para sa isang ≥ c. Ang paghila ng thread gamit ang isang lapis, gumuhit ng isang linya, na magiging isang ellipse (Larawan 7.1).
Kaya, ang inilarawan na set ay hindi walang laman kung ang isang ≥ c. Kapag a = c, ang ellipse ay isang segment na may dulo ng F 1 at F 2, at kapag c = 0, i.e. kung ang mga nakapirming puntos na tinukoy sa kahulugan ng isang ellipse ay nag-tutugma, ito ay isang bilog ng radius a. Kung itinatapon ang mga lumalalang kaso na ito, ipagpalagay pa namin, bilang panuntunan, na a > c > 0.
Ang mga nakapirming puntos na F 1 at F 2 sa kahulugan 7.1 ng ellipse (tingnan ang Fig. 7.1) ay tinatawag ellipse tricks, ang distansya sa pagitan nila, na tinutukoy ng 2c, - Focal length, at ang mga segment na F 1 M at F 2 M, na nagkokonekta sa isang di-makatwirang punto M sa ellipse kasama ang foci nito, - focal radii.
Ang anyo ng ellipse ay ganap na tinutukoy ng focal length |F 1 F 2 | = 2с at parameter a, at ang posisyon nito sa eroplano - sa pamamagitan ng isang pares ng mga puntos F 1 at F 2 .
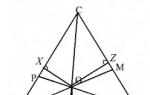
Ito ay sumusunod mula sa kahulugan ng isang ellipse na ito ay simetriko tungkol sa isang tuwid na linya na dumadaan sa foci F 1 at F 2, pati na rin tungkol sa isang tuwid na linya na naghahati sa segment na F 1 F 2 sa kalahati at patayo dito (Fig 7.2, a). Ang mga linyang ito ay tinatawag ellipse axes. Ang punto O ng kanilang intersection ay ang sentro ng simetrya ng ellipse, at ito ay tinatawag ang gitna ng ellipse, at ang mga punto ng intersection ng ellipse na may mga axes ng simetrya (mga punto A, B, C at D sa Fig. 7.2, a) - ang mga vertex ng ellipse.

Ang numero a ay tinatawag semi-major axis ng isang ellipse, at b = √ (a 2 - c 2) - nito semi-minor na axis. Madaling makita na para sa c > 0, ang pangunahing semiaxis a ay katumbas ng distansya mula sa gitna ng ellipse hanggang sa mga vertices nito na nasa parehong axis ng foci ng ellipse (vertices A at B sa Fig 7.2, a), at ang minor semiaxis b ay katumbas ng distansya mula sa gitnang ellipse hanggang sa iba pang dalawang vertices nito (mga vertices C at D sa Fig. 7.2, a).
Ellipse equation. Isaalang-alang ang ilang ellipse sa eroplano na may foci sa mga puntong F 1 at F 2 , pangunahing axis 2a. Hayaang 2c ang focal length, 2c = |F 1 F 2 |
Pumili kami ng isang hugis-parihaba na coordinate system na Oxy sa eroplano upang ang pinagmulan nito ay tumutugma sa gitna ng ellipse, at ang foci ay nasa abscissa(Larawan 7.2, b). Ang coordinate system na ito ay tinatawag kanonikal para sa ellipse na isinasaalang-alang, at ang kaukulang mga variable ay kanonikal.
Sa napiling coordinate system, ang foci ay may mga coordinate F 1 (c; 0), F 2 (-c; 0). Gamit ang formula para sa distansya sa pagitan ng mga punto, isinusulat namin ang kondisyon |F 1 M| + |F 2 M| = 2a sa mga coordinate:
√((x - c) 2 + y 2) + √((x + c) 2 + y 2) = 2a. (7.2)
Ang equation na ito ay hindi maginhawa dahil naglalaman ito ng dalawang square radical. Kaya't ibahin natin ito. Ilipat natin ang pangalawang radical sa equation (7.2) sa kanang bahagi at parisukat ito:
(x - c) 2 + y 2 = 4a 2 - 4a√((x + c) 2 + y 2) + (x + c) 2 + y 2 .
Pagkatapos buksan ang mga bracket at bawasan ang mga katulad na termino, nakukuha namin
√((x + c) 2 + y 2) = a + εx
kung saan ε = c/a. Inuulit namin ang squaring operation upang alisin ang pangalawang radical: (x + c) 2 + y 2 = a 2 + 2εax + ε 2 x 2, o, na ibinigay ang halaga ng ipinasok na parameter ε, (a 2 - c 2) x 2 / a 2 + y 2 = a 2 - c 2 . Dahil ang isang 2 - c 2 = b 2 > 0, kung gayon
x 2 /a 2 + y 2 /b 2 = 1, a > b > 0. (7.4)
Ang equation (7.4) ay nasiyahan sa pamamagitan ng mga coordinate ng lahat ng mga punto na nakahiga sa ellipse. Ngunit kapag hinango ang equation na ito, ginamit ang walang katumbas na pagbabago ng orihinal na equation (7.2) - dalawang parisukat na nag-aalis ng mga square radical. Ang pag-square ng isang equation ay isang katumbas na pagbabagong-anyo kung ang magkabilang panig ay naglalaman ng mga dami na may parehong tanda, ngunit hindi namin ito nasuri sa aming mga pagbabago.
Maaaring hindi namin suriin ang pagkakapareho ng mga pagbabago kung isasaalang-alang namin ang mga sumusunod. Isang pares ng mga puntos F 1 at F 2 , |F 1 F 2 | = 2c, sa eroplano ay tumutukoy sa isang pamilya ng mga ellipse na may foci sa mga puntong ito. Ang bawat punto ng eroplano, maliban sa mga punto ng segment na F 1 F 2 , ay kabilang sa ilang ellipse ng ipinahiwatig na pamilya. Sa kasong ito, walang dalawang ellipse ang nagsalubong, dahil ang kabuuan ng focal radii ay natatanging tumutukoy sa isang partikular na ellipse. Kaya, ang inilarawan na pamilya ng mga ellipse na walang mga intersection ay sumasaklaw sa buong eroplano, maliban sa mga punto ng segment F 1 F 2 . Isaalang-alang ang isang hanay ng mga puntos na ang mga coordinate ay nakakatugon sa equation (7.4) na may ibinigay na halaga ng parameter a. Maaari bang ipamahagi ang set na ito sa ilang ellipses? Ang ilan sa mga punto ng set ay nabibilang sa isang ellipse na may semi-major axis a. Hayaang mayroong isang punto sa set na ito na nakahiga sa isang ellipse na may semi-major axis a. Pagkatapos ang mga coordinate ng puntong ito ay sumunod sa equation
mga. ang mga equation (7.4) at (7.5) ay mayroon pangkalahatang solusyon. Gayunpaman, madaling i-verify na ang system

para sa ã ≠ a ay walang mga solusyon. Upang gawin ito, sapat na upang ibukod, halimbawa, ang x mula sa unang equation:

na pagkatapos ng mga pagbabago ay humahantong sa equation

walang mga solusyon para sa ã ≠ a, dahil . Kaya, ang (7.4) ay ang equation ng isang ellipse na may major semi-axis a > 0 at isang minor semi-axis b = √ (a 2 - c 2) > 0. Ito ay tinatawag ang canonical equation ng ellipse.
Ellipse view. Ang geometric na paraan ng pagbuo ng isang ellipse na isinasaalang-alang sa itaas ay nagbibigay ng sapat na ideya ng hitsura ellipse. Ngunit ang anyo ng isang ellipse ay maaari ding maimbestigahan sa tulong ng canonical equation nito (7.4). Halimbawa, kung isasaalang-alang ang y ≥ 0, maaari mong ipahayag ang y sa mga tuntunin ng x: y = b√(1 - x 2 /a 2), at, nang masuri ang function na ito, buuin ang graph nito. May isa pang paraan upang makagawa ng isang ellipse. Ang isang bilog ng radius a na nakasentro sa pinagmulan ng canonical coordinate system ng ellipse (7.4) ay inilalarawan ng equation x 2 + y 2 = a 2 . Kung ito ay naka-compress sa coefficient a/b > 1 kasama y-axis, pagkatapos ay makakakuha ka ng curve na inilalarawan ng equation x 2 + (ya / b) 2 \u003d a 2, i.e. isang ellipse.
Puna 7.1. Kung ang parehong bilog ay na-compress na may coefficient a/b
Ellipse eccentricity. Saloobin Focal length ellipse sa pangunahing axis nito ay tinatawag ellipse eccentricity at tinutukoy ng ε. Para sa isang ellipse na ibinigay

canonical equation (7.4), ε = 2c/2a = с/a. Kung sa (7.4) ang mga parameter a at b ay nauugnay sa hindi pagkakapantay-pantay a
Para sa c = 0, kapag ang ellipse ay naging bilog, at ε = 0. Sa ibang mga kaso, 0
Ang equation (7.3) ay katumbas ng equation (7.4) dahil ang mga equation (7.4) at (7.2) ay katumbas. Samakatuwid, ang (7.3) ay isa ring ellipse equation. Bilang karagdagan, ang kaugnayan (7.3) ay kawili-wili dahil nagbibigay ito ng simpleng formula na walang radikal para sa haba |F 2 M| isa sa focal radii ng point M(x; y) ng ellipse: |F 2 M| = a + εx.
Ang isang katulad na formula para sa pangalawang focal radius ay maaaring makuha mula sa mga pagsasaalang-alang sa symmetry o sa pamamagitan ng paulit-ulit na mga kalkulasyon kung saan, bago ang squaring equation (7.2), ang unang radical ay inililipat sa kanang bahagi, at hindi ang pangalawa. Kaya, para sa anumang punto M(x; y) sa ellipse (tingnan ang Fig. 7.2)
|F 1 M | = a - εx, |F 2 M| = a + εx, (7.6)
at bawat isa sa mga equation na ito ay isang ellipse equation.
Halimbawa 7.1. Hanapin natin canonical equation ellipse na may semi-major axis 5 at eccentricity 0.8 at buuin ito.
Alam ang major semiaxis ng ellipse a = 5 at ang eccentricity ε = 0.8, makikita natin ang minor semiaxis b nito. Dahil b \u003d √ (a 2 - c 2), at c \u003d εa \u003d 4, pagkatapos b \u003d √ (5 2 - 4 2) \u003d 3. Kaya ang canonical equation ay may anyo x 2 / 5 2 + y 2 / 3 2 \u003d 1. Upang makabuo ng isang ellipse, ito ay maginhawa upang gumuhit ng isang rektanggulo na nakasentro sa pinagmulan ng canonical coordinate system, ang mga gilid nito ay kahanay sa mga axes ng simetrya ng ellipse at katumbas nito kaukulang axes (Larawan 7.4). Ang parihaba na ito ay bumalandra sa

ang mga palakol ng ellipse sa mga vertice nito A(-5; 0), B(5; 0), C(0; -3), D(0; 3), at ang ellipse mismo ay nakasulat dito. Sa fig. Ipinapakita rin ng 7.4 ang foci F 1.2 (±4; 0) ng ellipse.
Mga geometric na katangian ng isang ellipse. Isulat muli natin ang unang equation sa (7.6) bilang |F 1 M| = (а/ε - x)ε. Tandaan na ang halaga ng a / ε - x ay positibo para sa a > c, dahil ang focus F 1 ay hindi kabilang sa ellipse. Ang halagang ito ay ang distansya sa patayong linya d: x = a/ε mula sa puntong M(x; y) sa kaliwa ng linyang ito. Ang ellipse equation ay maaaring isulat bilang
|F 1 M|/(а/ε - x) = ε
Nangangahulugan ito na ang ellipse na ito ay binubuo ng mga puntong M (x; y) ng eroplano kung saan ang ratio ng haba ng focal radius F 1 M sa distansya sa tuwid na linya d ay isang pare-parehong halaga na katumbas ng ε (Fig. 7.5).

Ang linya d ay may "doble" - isang patayong linya d", simetriko sa d na may paggalang sa gitna ng ellipse, na ibinibigay ng equation x \u003d -a / ε. Sa paggalang sa d", ang ellipse ay inilarawan sa parehong paraan tulad ng tungkol sa d. Parehong linya d at d" ay tinatawag ellipse directrix. Ang mga directrix ng ellipse ay patayo sa axis ng symmetry ng ellipse, kung saan matatagpuan ang foci nito, at pinaghihiwalay mula sa gitna ng ellipse sa isang distansya a / ε \u003d a 2 / c (tingnan ang Fig. 7.5) .
Tinatawag ang distansya p mula sa directrix hanggang sa pokus na pinakamalapit dito focal parameter ng ellipse. Ang parameter na ito ay katumbas ng
p \u003d a / ε - c \u003d (a 2 - c 2) / c \u003d b 2 / c
Ang ellipse ay may isa pang mahalagang geometric na katangian: ang focal radii F 1 M at F 2 M ay padaplis sa ellipse sa punto M pantay na anggulo(Larawan 7.6).

Ang ari-arian na ito ay may malinaw pisikal na kahulugan. Kung ang isang pinagmumulan ng liwanag ay inilagay sa focus F 1, kung gayon ang sinag na lumalabas mula sa pokus na ito, pagkatapos ng pagmuni-muni mula sa ellipse, ay pupunta sa pangalawang focal radius, dahil pagkatapos ng pagmuni-muni ito ay nasa parehong anggulo sa kurba tulad ng bago ang pagmuni-muni . Kaya, ang lahat ng mga sinag na umaalis sa focus F 1 ay mapupunta sa pangalawang focus F 2 at vice versa. Batay sa interpretasyong ito, ang ari-arian na ito ay tinatawag optical property ng isang ellipse.
Mga kurba ng pangalawang pagkakasunud-sunod sa isang eroplano ay tinatawag na mga linya na tinukoy ng mga equation kung saan ang mga variable na coordinate x at y nakapaloob sa ikalawang antas. Kabilang dito ang ellipse, hyperbola, at parabola.
Ang pangkalahatang anyo ng second-order curve equation ay ang mga sumusunod:
saan A, B, C, D, E, F- mga numero at hindi bababa sa isa sa mga coefficient A, B, C ay hindi katumbas ng zero.
Kapag nilulutas ang mga problema sa second-order curves, ang mga canonical equation ng isang ellipse, hyperbola, at parabola ay kadalasang isinasaalang-alang. Madaling ipasa sa kanila mula sa mga pangkalahatang equation, ang halimbawa 1 ng mga problema sa mga ellipse ay iuukol dito.
Ellipse na ibinigay ng canonical equation
Kahulugan ng isang ellipse. Ang isang ellipse ay ang hanay ng lahat ng mga punto sa eroplano, ang mga kung saan ang kabuuan ng mga distansya sa mga punto, na tinatawag na foci, ay pare-pareho at mas malaki kaysa sa distansya sa pagitan ng foci.
Ang mga focus ay minarkahan tulad ng nasa figure sa ibaba.
Ang canonical equation ng isang ellipse ay:
saan a at b (a > b) - ang mga haba ng semiaxes, ibig sabihin, kalahati ng haba ng mga segment na pinutol ng ellipse sa coordinate axes.

Ang tuwid na linya na dumadaan sa foci ng ellipse ay ang axis ng symmetry nito. Ang isa pang axis ng symmetry ng ellipse ay isang tuwid na linya na dumadaan sa gitna ng segment na patayo sa segment na ito. Dot O ang intersection ng mga linyang ito ay nagsisilbing sentro ng simetrya ng ellipse, o simpleng sentro ng ellipse.
Ang abscissa axis ng ellipse ay nagsalubong sa mga punto ( a, O) at (- a, O), at ang y-axis ay nasa mga punto ( b, O) at (- b, O). Ang apat na puntong ito ay tinatawag na vertices ng ellipse. Ang segment sa pagitan ng mga vertices ng ellipse sa abscissa axis ay tinatawag na major axis nito, at sa ordinate axis - ang minor axis. Ang kanilang mga segment mula sa itaas hanggang sa gitna ng ellipse ay tinatawag na semiaxes.
Kung ang a = b, pagkatapos ay ang equation ng ellipse ay kukuha ng anyo . Ito ang equation para sa isang bilog ng radius a, at ang bilog ay isang espesyal na kaso ng isang ellipse. Ang isang ellipse ay maaaring makuha mula sa isang bilog ng radius a, kung i-compress mo ito sa a/b beses sa kahabaan ng axis Oy .
Halimbawa 1 Suriin kung ang linya na ibinigay ng pangkalahatang equation ![]() , isang ellipse.
, isang ellipse.
Desisyon. Gumagawa kami ng mga pagbabago pangkalahatang equation. Inilapat namin ang paglipat ng libreng termino sa kanang bahagi, ang termino-by-term na dibisyon ng equation sa pamamagitan ng parehong numero at ang pagbabawas ng mga fraction:

Sagot. Ang resultang equation ay ang canonical equation ng ellipse. Samakatuwid, ang linyang ito ay isang ellipse.
Halimbawa 2 Isulat ang canonical equation ng isang ellipse kung ang mga semiax nito ay 5 at 4, ayon sa pagkakabanggit.
Desisyon. Tinitingnan natin ang formula para sa canonical equation ng ellipse at substitute: ang semi-major axis ay a= 5 , ang minor semiaxis ay b= 4 . Nakukuha namin ang canonical equation ng ellipse:
Mga puntos at minarkahan ng berde sa pangunahing axis, kung saan
tinawag mga trick.
tinawag eccentricity ellipse.
Saloobin b/a nailalarawan ang "oblateness" ng ellipse. Kung mas maliit ang ratio na ito, mas pinalawak ang ellipse sa kahabaan ng major axis. Gayunpaman, ang antas ng pagpahaba ng ellipse ay mas madalas na ipinahayag sa mga tuntunin ng eccentricity, ang formula na ibinigay sa itaas. Para sa iba't ibang mga ellipse, ang eccentricity ay nag-iiba mula 0 hanggang 1, palaging nananatiling mas mababa sa isa.
Halimbawa 3 Isulat ang canonical equation ng isang ellipse kung ang distansya sa pagitan ng foci ay 8 at ang major axis ay 10.
Desisyon. Gumagawa kami ng mga simpleng konklusyon:
Kung ang pangunahing axis ay 10, ang kalahati nito, i.e. semiaxis a = 5 ,
Kung ang distansya sa pagitan ng foci ay 8, kung gayon ang numero c sa mga focus coordinate ay 4.
Palitan at kalkulahin:

Ang resulta ay ang canonical equation ng ellipse:
Halimbawa 4 Isulat ang canonical equation ng isang ellipse kung ang major axis nito ay 26 at ang eccentricity ay .
Desisyon. Tulad ng mga sumusunod mula sa parehong sukat ng pangunahing axis at ang eccentricity equation, ang pangunahing semiaxis ng ellipse a= 13 . Mula sa eccentricity equation, ipinapahayag namin ang numero c, kailangan upang kalkulahin ang haba ng menor de edad na semiaxis:
![]() .
.
Kinakalkula namin ang parisukat ng haba ng menor de edad na semiaxis:

Binubuo namin ang canonical equation ng ellipse:
Halimbawa 5 Tukuyin ang foci ng ellipse na ibinigay ng canonical equation.
Desisyon. Kailangang maghanap ng numero c, na tumutukoy sa mga unang coordinate ng foci ng ellipse:
![]() .
.
Nakukuha namin ang mga pokus ng ellipse:
![]()
Halimbawa 6 Ang foci ng ellipse ay matatagpuan sa axis baka simetriko tungkol sa pinagmulan. Isulat ang canonical equation ng isang ellipse kung:
1) ang distansya sa pagitan ng foci ay 30, at pangunahing axis 34
2) ang minor axis ay 24, at ang isa sa mga nakatutok ay nasa punto (-5; 0)
3) eccentricity, at ang isa sa mga foci ay nasa punto (6; 0)
Patuloy naming nilulutas ang mga problema sa ellipse nang magkasama
Kung - isang di-makatwirang punto ng ellipse (minarkahan ng berde sa pagguhit sa kanang itaas na bahagi ng ellipse) at - ang mga distansya sa puntong ito mula sa foci, kung gayon ang mga formula para sa mga distansya ay ang mga sumusunod:
Para sa bawat punto na kabilang sa ellipse, ang kabuuan ng mga distansya mula sa foci ay isang pare-parehong halaga na katumbas ng 2 a.
Mga tuwid na linya na tinukoy ng mga equation
tinawag mga direktor ellipse (sa pagguhit - mga pulang linya sa mga gilid).
Mula sa dalawang equation sa itaas ay sumusunod na para sa anumang punto ng ellipse
![]() ,
,
kung saan at ang mga distansya ng puntong ito sa mga directrix at .
Halimbawa 7 Binigyan ng ellipse. Sumulat ng isang equation para sa mga directrix nito.
Desisyon. Tinitingnan namin ang directrix equation at nalaman na kinakailangan upang mahanap ang eccentricity ng ellipse, ibig sabihin. Ang lahat ng data para dito ay. Kinakalkula namin:
 .
.
Nakukuha namin ang equation ng directrix ng ellipse:
![]()
Halimbawa 8 Isulat ang canonical equation ng isang ellipse kung ang foci nito ay mga puntos at ang mga directrix ay mga linya.
Ang canonical equation ng isang ellipse ay may anyo
kung saan ang a ay ang semi-major axis; b - menor de edad na semiaxis. Ang mga puntos na F1(c,0) at F2(-c,0) − c ay tinatawag

a, b - mga semiax ng ellipse.
Paghahanap ng foci, eccentricity, directrix ng isang ellipse kung alam ang canonical equation nito.
Kahulugan ng hyperbola. Foci ng hyperbole.
Kahulugan. Ang hyperbola ay isang hanay ng mga punto sa isang eroplano kung saan ang modulus ng pagkakaiba sa mga distansya mula sa dalawang ibinigay na mga punto, na tinatawag na foci, ay isang pare-parehong halaga, mas mababa kaysa sa distansya sa pagitan ng foci.

Sa kahulugan, |r1 – r2|= 2a. Ang F1, F2 ay ang foci ng hyperbola. F1F2 = 2c.
Ang canonical equation ng isang hyperbola. Mga semiax ng hyperbola. Pagbubuo ng hyperbola kung alam ang canonical equation nito.
Canonical equation:
Ang semi-major axis ng hyperbola ay kalahati ng pinakamababang distansya sa pagitan ng dalawang sangay ng hyperbola, sa positibo at negatibong panig axes (kaliwa at kanan na nauugnay sa pinanggalingan). Para sa sangay na matatagpuan sa positibong panig, ang semiaxis ay magiging katumbas ng:
![]()
Kung ipahayag natin ito sa mga tuntunin ng conic section at ang eccentricity, ang expression ay kukuha ng form:
Paghahanap ng foci, eccentricity, directrix ng isang hyperbola kung alam ang canonical equation nito.
Eccentricity ng isang hyperbola
Kahulugan. Ang ratio ay tinatawag na eccentricity ng hyperbola, kung saan c -
kalahati ng distansya sa pagitan ng foci, at ang tunay na semiaxis.
Isinasaalang-alang ang katotohanan na c2 - a2 = b2:
Kung a \u003d b, e \u003d, kung gayon ang hyperbola ay tinatawag na equilateral (equilateral).
Directtrix ng hyperbole
Kahulugan. Dalawang linya na patayo sa totoong axis ng hyperbola at matatagpuan sa simetriko tungkol sa gitna sa layo na a / e mula dito ay tinatawag na mga directrix ng hyperbola. Ang kanilang mga equation ay:
Teorama. Kung ang r ay ang distansya mula sa isang arbitrary na punto M ng hyperbola sa ilang focus, ang d ay ang distansya mula sa parehong punto hanggang sa directrix na naaayon sa focus na ito, kung gayon ang ratio r/d ay isang pare-parehong halaga na katumbas ng eccentricity.
Kahulugan ng isang parabola. Focus at directix ng isang parabola.
Parabola. Ang parabola ay ang locus ng mga puntos, na ang bawat isa ay pantay na malayo sa isang takdang punto at mula sa isang takdang linya. Ang punto tungkol sa kung saan sa tanong sa kahulugan, ay tinatawag na pokus ng parabola, at ang tuwid na linya ay tinatawag na directrix nito.
Ang canonical equation ng isang parabola. parameter ng parabola. Paggawa ng isang parabola.
Ang canonical equation ng isang parabola sa isang rectangular coordinate system ay: (o kung ang mga axes ay baligtad).
Paggawa ng parabola para sa binigay na halaga Ang parameter p ay isinasagawa sa sumusunod na pagkakasunud-sunod:
Iguhit ang axis ng symmetry ng parabola at ilagay dito ang segment na KF=p;
Ang Directrix DD1 ay iginuhit sa pamamagitan ng puntong K patayo sa axis ng simetrya;
Ang segment na KF ay hinati sa kalahati upang makuha ang vertex 0 ng parabola;
Ang isang bilang ng mga arbitrary na puntos 1, 2, 3, 5, 6 ay sinusukat mula sa itaas na may unti-unting pagtaas ng distansya sa pagitan nila;
Sa pamamagitan ng mga puntong ito, ang mga auxiliary na linya ay iginuhit patayo sa axis ng parabola;
Sa mga pantulong na tuwid na linya, ang mga serif ay ginawa na may radius na katumbas ng distansya mula sa tuwid na linya hanggang sa directrix;
Ang mga nagresultang punto ay konektado sa pamamagitan ng isang makinis na kurba.
Kahulugan. Ang isang ellipse ay ang locus ng mga puntos sa isang eroplano, ang kabuuan ng mga distansya ng bawat isa sa kanila mula sa dalawang ibinigay na mga punto ng eroplanong ito, na tinatawag na foci, ay isang pare-parehong halaga (sa kondisyon na ang halagang ito ay mas malaki kaysa sa distansya sa pagitan ng foci).
Tukuyin natin ang foci sa pamamagitan ng distansya sa pagitan nila - through , at ang pare-parehong halaga, katumbas ng kabuuan mga distansya mula sa bawat punto ng ellipse hanggang sa foci, sa pamamagitan ng (ayon sa kondisyon ).
Bumuo tayo ng isang Cartesian coordinate system upang ang foci ay nasa abscissa axis, at ang pinagmulan ng mga coordinate ay tumutugma sa gitna ng segment (Fig. 44). Pagkatapos ang mga focus ay magkakaroon ng mga sumusunod na coordinate: kaliwang focus at kanang focus. Kunin natin ang equation ng ellipse sa coordinate system na napili natin. Sa layuning ito, isaalang-alang ang isang arbitrary na punto ng ellipse. Sa pamamagitan ng kahulugan ng isang ellipse, ang kabuuan ng mga distansya mula sa puntong ito hanggang sa foci ay:
![]()
Gamit ang formula para sa distansya sa pagitan ng dalawang puntos, nakukuha namin, samakatuwid,
Upang gawing simple ang equation na ito, isinusulat namin ito sa form
Pagkatapos ay nagbibigay ang pag-squaring sa magkabilang panig ng equation
o, pagkatapos ng malinaw na pagpapasimple:
Ngayon muli naming parisukat ang magkabilang panig ng equation, pagkatapos nito ay magkakaroon kami ng:
o, pagkatapos ng magkatulad na pagbabago:
Dahil ayon sa kondisyon sa kahulugan ng isang ellipse , kung gayon ay isang positibong numero. Ipinakilala namin ang notasyon
Pagkatapos ang equation ay kukuha ng sumusunod na anyo:
![]()
Sa pamamagitan ng kahulugan ng isang ellipse, ang mga coordinate ng alinman sa mga punto nito ay nakakatugon sa equation (26). Ngunit ang equation (29) ay bunga ng equation (26). Samakatuwid, natutugunan din nito ang mga coordinate ng anumang punto ng ellipse.
Maaaring ipakita na ang mga coordinate ng mga puntos na hindi nakahiga sa ellipse ay hindi nakakatugon sa equation (29). Kaya, ang equation (29) ay ang equation ng isang ellipse. Ito ay tinatawag na canonical equation ng ellipse.
Itatag natin ang hugis ng ellipse gamit ang canonical equation nito.
Una sa lahat, tandaan na ang equation na ito ay naglalaman lamang ng kahit na mga kapangyarihan ng x at y. Nangangahulugan ito na kung ang anumang punto ay kabilang sa isang ellipse, kasama rin dito ang isang punto na simetriko na may isang punto tungkol sa abscissa axis, at isang punto na simetriko na may isang punto tungkol sa y-axis. Kaya, ang ellipse ay may dalawang magkaparehong patayo na axes ng symmetry, na sa aming napiling coordinate system ay nag-tutugma sa mga coordinate axes. Ang mga axes ng symmetry ng ellipse ay tatawaging axes ng ellipse, at ang punto ng kanilang intersection - ang gitna ng ellipse. Ang axis kung saan matatagpuan ang foci ng ellipse (sa kasong ito, ang abscissa axis) ay tinatawag na focal axis.
Tukuyin muna natin ang hugis ng ellipse sa unang quarter. Upang gawin ito, lutasin namin ang equation (28) na may paggalang sa y:
![]()
Ito ay malinaw na dito , dahil ang y ay kumukuha ng mga haka-haka na halaga para sa . Sa pagtaas mula 0 hanggang a, ang y ay bumababa mula b hanggang 0. Ang bahagi ng ellipse na nakahiga sa unang quarter ay magiging isang arko na nililimitahan ng mga puntos na B (0; b) at nakahiga sa mga coordinate axes (Fig. 45). Gamit ngayon ang simetrya ng ellipse, napagpasyahan namin na ang ellipse ay may hugis na ipinapakita sa Fig. 45.

Ang mga punto ng intersection ng ellipse na may mga axes ay tinatawag na vertices ng ellipse. Ito ay sumusunod mula sa simetrya ng ellipse na, bilang karagdagan sa mga vertices, ang ellipse ay may dalawa pang vertices (tingnan ang Fig. 45).
Ang mga segment at pagkonekta sa magkasalungat na vertices ng ellipse, pati na rin ang kanilang mga haba, ay tinatawag na major at minor axes ng ellipse, ayon sa pagkakabanggit. Ang mga numerong a at b ay tinatawag na major at minor semiax ng ellipse, ayon sa pagkakabanggit.
Ang ratio ng kalahati ng distansya sa pagitan ng foci hanggang sa semi-major axis ng ellipse ay tinatawag na eccentricity ng ellipse at karaniwang tinutukoy ng titik:
Dahil , kung gayon ang eccentricity ng ellipse ay mas mababa sa isa: Ang eccentricity ay nagpapakilala sa hugis ng ellipse. Sa katunayan, ito ay sumusunod mula sa formula (28), Mula dito makikita na mas maliit ang eccentricity ng ellipse, mas mababa ang minor semiaxis b nito mula sa major semiaxis a, ibig sabihin, mas maliit ang ellipse ay pinalawak (kasama ang focal aksis).
Sa limitadong kaso, kapag nakakuha ka ng bilog na radius a: , o . Kasabay nito, ang foci ng ellipse, tulad nito, ay pinagsama sa isang punto - ang gitna ng bilog. Ang eccentricity ng bilog ay zero:
Ang koneksyon sa pagitan ng ellipse at ng bilog ay maaaring maitatag mula sa ibang punto ng view. Ipakita natin na ang isang ellipse na may mga semi-axes a at b ay maituturing na projection ng isang bilog na radius a.
Isaalang-alang natin ang dalawang eroplanong P at Q, na bumubuo ng gayong anggulo sa pagitan ng kanilang mga sarili, kung saan (Larawan 46). Buuin natin sa plane P ang coordinate system , at sa plane Q - ang system Oxy with karaniwang simula coordinate O at karaniwang axis abscissa na kasabay ng linya ng intersection ng mga eroplano. Isaalang-alang sa eroplano P ang bilog
![]()
nakasentro sa pinanggalingan at radius a. Hayaang maging isang arbitraryong napiling punto ng bilog, maging projection nito sa Q plane, at maging projection ng point M papunta sa Ox axis. Ipakita natin na ang punto ay nasa isang ellipse na may mga semi-axes a at b.